Capítulo 1 Experimentos fatoriais completamente cruzados gerais
Em CE 074 · Controle de Processos Industriais serão estudados os experimentos fatoriais com ênfase nos \(2^k\) e \(3^k\). Todavia, antes de partir para esses delineamentos particulares, será visto os experimentos fatoriais gerais. Nestes estuda-se \(k \geq 2\) fatores simultâneamente, cada um com \(n_i\) níveis (\(i = 1, \ldots, k)\) com todas as combinações entre níveis presentes no experimento.
O presente capítulo irá apresentar a análise do experimento fatorial duplo (\(k = 2\)) com fatores qualitativos.
# Carrega pacotes.
library(emmeans)
library(tidyverse)1.1 Fatorial duplo · Bateria
Os dados usados nesta seção referem-se àqueles disponíveis em MONTGOMERY (2008). O experimento foi feito por um engenheiro que estava projetando uma bateria para um dispositivo que estaria sujeito à variações extremas de temperatura. Visando projetar uma bateria com prolongado tempo de vida, o experimentador escolheu 3 materiais para confecção das baterias e nos testes, submeteu as baterias à 3 níveis de temperatura para mensurar o tempo de vida, em horas. Cada ponto experimental teve 4 repetições. As 36 unidades experimentais foram avaliadas em ordem aleatória.
- Página da editora sobre o livro: https://www.wiley.com/en-us/Design+and+Analysis+of+Experiments%2C+10th+Edition-p-9781119492443.
- Material suplementar: http://bcs.wiley.com/he-bcs/Books?action=index&itemId=1119492440&bcsId=11447.
Na seção a seguir é feita a análise exploratória dos dados.
1.1.1 Análise exploratória
# Tempo de duração da bateria. Tabela 5.1 em Montgomery (2008).
tv <- c(130, 74, 150, 159, 138, 168, 155, 180, 188, 126, 110, 160, 34,
80, 136, 106, 174, 150, 40, 75, 122, 115, 120, 139, 20, 82, 25,
58, 96, 82, 70, 58, 70, 45, 104, 60)
temp <- rep(c(15, 70, 125), each = 12)
mate <- rep(rep(c(1:3), each = 2), times = 6)
# Cria tabela com os dados.
tb <- data.frame(temp = factor(temp),
mate = factor(mate),
tv = tv)
# Remove vetores do espaço de memória.
rm(tv, temp, mate)
# Número de repetições dos pontos experimentais.
xtabs(~mate + temp, data = tb)## temp
## mate 15 70 125
## 1 4 4 4
## 2 4 4 4
## 3 4 4 4ggplot(data = tb,
mapping = aes(x = temp, color = mate, y = tv)) +
geom_point() +
stat_summary(aes(group = mate), geom = "line", fun.y = "mean") +
labs(x = "Temperatura (°C)",
y = "Tempo de vida (h)",
color = "Material")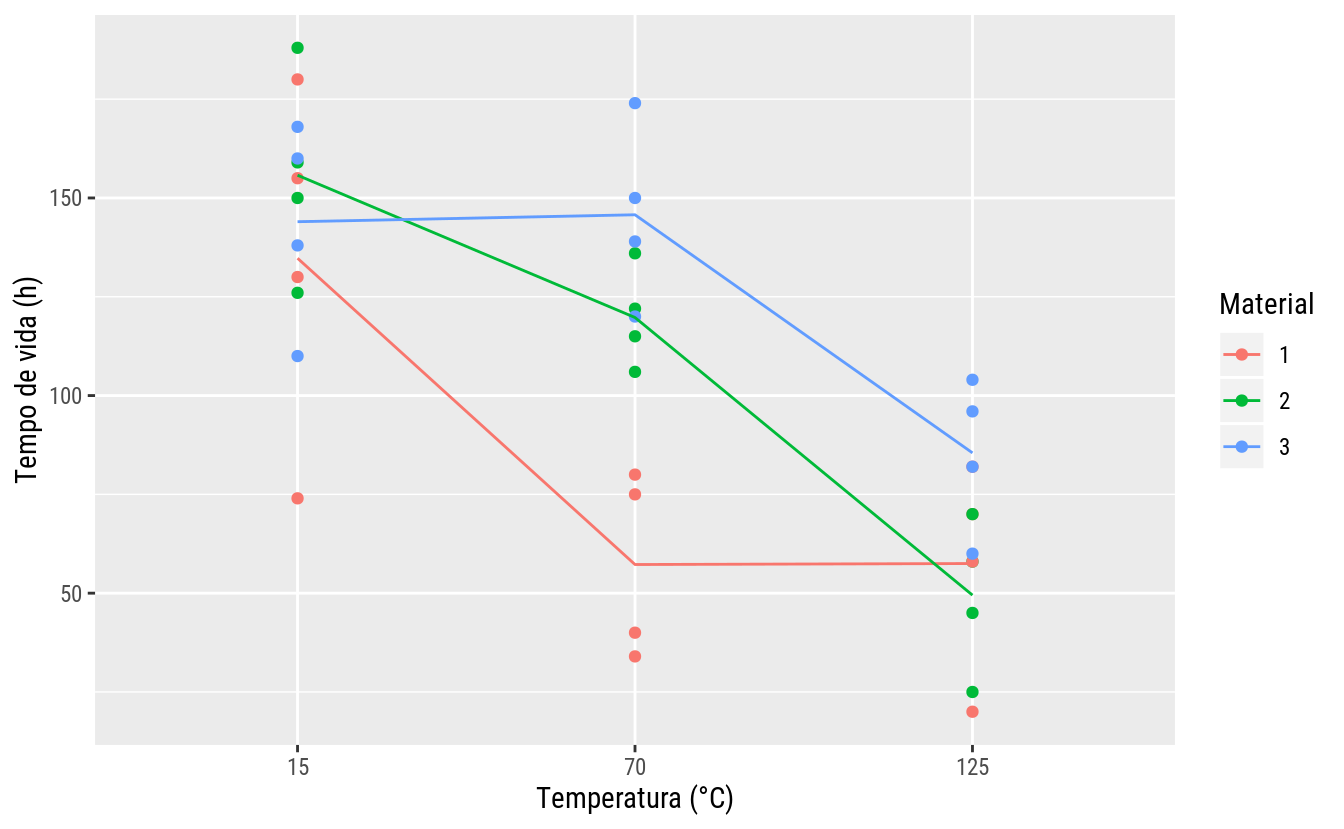
ggplot(data = tb,
mapping = aes(x = mate, color = temp, y = tv)) +
geom_point() +
stat_summary(aes(group = temp), geom = "line", fun.y = "mean") +
labs(x = "Material",
y = "Tempo de vida (h)",
color = "Temperatura (°C)")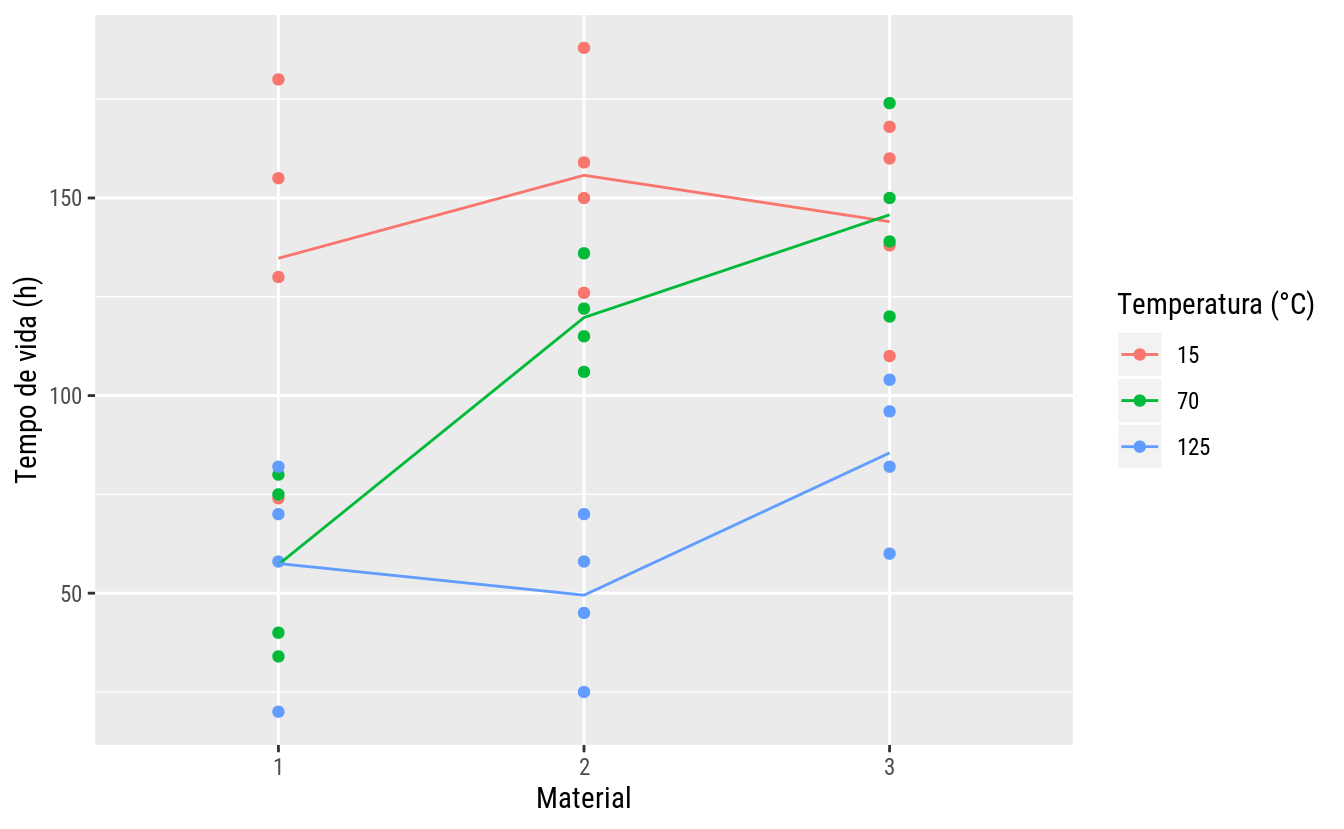
1.1.2 Especificação e ajuste do modelo
O modelo estatístico para esse experimento, considerando ambos fatores como qualitativos e conduzido sob o delineamento inteiramente casualizado, é \[ \begin{aligned} y_{ijk} &\sim \text{Normal}(\mu_{ij}, \sigma^2) \\ \mu_{ij} &= \mu + \tau_i + \theta_j + \gamma_{ij}\\ \sigma^2 &\propto 1 \end{aligned} \] em que \(y_{ijk}\) é o valor observado para o ponto experimental do material \(i\) e temperatura \(j\) na repetição \(k\), \(\mu\) é uma constante inerente à todas as observações, \(\tau_i\) são parâmetros para acomodar o efeito de material, \(\theta_j\) são parâmetros para acomodar o efeito de temperatura e \(\gamma_{ij}\) são parâmetros para acomodar a interação entre material e temperatura.
O código abaixo faz o ajuste do modelo aos dados usando a restrição de zerar o efeito do primeiro nível do fator. Portanto, a interpretação dos parâmetros está vinculada a essas restrições.
# Espeficicação do modelo para a função `lm()`.
m0 <- lm(tv ~ mate + temp + mate:temp, data = tb)
m0 <- lm(tv ~ mate * temp, data = tb) # Forma curta.
# Quadro de resumo do ajuste.
summary(m0)##
## Call:
## lm(formula = tv ~ mate * temp, data = tb)
##
## Residuals:
## Min 1Q Median 3Q Max
## -60.750 -14.625 1.375 17.938 45.250
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 134.75 12.99 10.371 6.46e-11 ***
## mate2 21.00 18.37 1.143 0.263107
## mate3 9.25 18.37 0.503 0.618747
## temp70 -77.50 18.37 -4.218 0.000248 ***
## temp125 -77.25 18.37 -4.204 0.000257 ***
## mate2:temp70 41.50 25.98 1.597 0.121886
## mate3:temp70 79.25 25.98 3.050 0.005083 **
## mate2:temp125 -29.00 25.98 -1.116 0.274242
## mate3:temp125 18.75 25.98 0.722 0.476759
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 25.98 on 27 degrees of freedom
## Multiple R-squared: 0.7652, Adjusted R-squared: 0.6956
## F-statistic: 11 on 8 and 27 DF, p-value: 9.426e-07# Análise gráfica dos pressupostos.
par(mfrow = c(2, 2)); plot(m0); layout(1)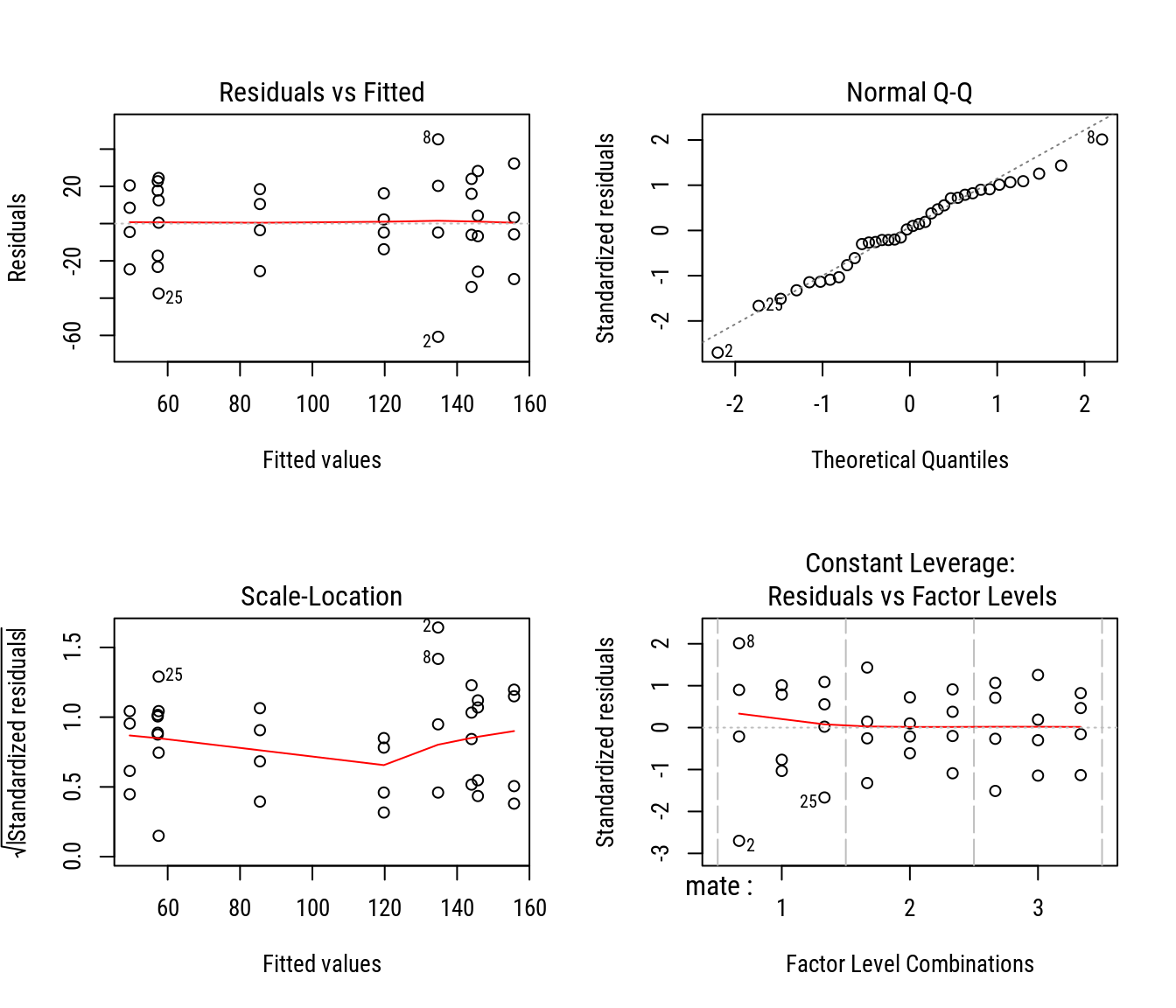
Os fragmento de código a seguir reproduz o que é retornado pela lm() com a finalidade de deixar explícitas as contas. As operações matriciais são feitas ipsis litteris as disponíveis nos livros. Por outro lado, não são a forma mais eficiente de implementar.
# Matriz do modelo.
X <- model.matrix(~mate * temp, data = tb)
# Indica o tipo de contraste usado.
attr(X, "contrasts")## $mate
## [1] "contr.treatment"
##
## $temp
## [1] "contr.treatment"# Vetor de observações.
y <- cbind(tb$tv)
# Estimativas dos parâmetros.
# coef(m0)
betas <- solve(t(X) %*% X, t(X) %*% y)
betas## [,1]
## (Intercept) 134.75
## mate2 21.00
## mate3 9.25
## temp70 -77.50
## temp125 -77.25
## mate2:temp70 41.50
## mate3:temp70 79.25
## mate2:temp125 -29.00
## mate3:temp125 18.75# Variância residual.
# deviance(m0)/df.residual(m0)
var_y <- crossprod(y - X %*% betas)/(nrow(X) - ncol(X))
# Matriz de covariância das estimativas.
# vcov(m0)
c(var_y) * solve(t(X) %*% X)## (Intercept) mate2 mate3 temp70 temp125
## (Intercept) 168.8032 -168.8032 -168.8032 -168.8032 -168.8032
## mate2 -168.8032 337.6065 168.8032 168.8032 168.8032
## mate3 -168.8032 168.8032 337.6065 168.8032 168.8032
## temp70 -168.8032 168.8032 168.8032 337.6065 168.8032
## temp125 -168.8032 168.8032 168.8032 168.8032 337.6065
## mate2:temp70 168.8032 -337.6065 -168.8032 -337.6065 -168.8032
## mate3:temp70 168.8032 -168.8032 -337.6065 -337.6065 -168.8032
## mate2:temp125 168.8032 -337.6065 -168.8032 -168.8032 -337.6065
## mate3:temp125 168.8032 -168.8032 -337.6065 -168.8032 -337.6065
## mate2:temp70 mate3:temp70 mate2:temp125 mate3:temp125
## (Intercept) 168.8032 168.8032 168.8032 168.8032
## mate2 -337.6065 -168.8032 -337.6065 -168.8032
## mate3 -168.8032 -337.6065 -168.8032 -337.6065
## temp70 -337.6065 -337.6065 -168.8032 -168.8032
## temp125 -168.8032 -168.8032 -337.6065 -337.6065
## mate2:temp70 675.2130 337.6065 337.6065 168.8032
## mate3:temp70 337.6065 675.2130 168.8032 337.6065
## mate2:temp125 337.6065 168.8032 675.2130 337.6065
## mate3:temp125 168.8032 337.6065 337.6065 675.2130Na seção a seguir é obtido o quadro de análise de variância.
1.1.3 O quadro de análise de variância
O quadro de análise de variância (ANOVA) tem a seguinte composição.
| FV | GL | E(MS) |
|---|---|---|
| A | \(a - 1\) | \(\sigma^2 + \frac{br \sum_i \tau_i^2}{a - 1}\) |
| B | \(b - 1\) | \(\sigma^2 + \frac{ar \sum_j \theta_j^2}{b - 1}\) |
| AB | \((a - 1)(b - 1)\) | \(\sigma^2 + \frac{r \sum_i \sum_j \gamma_{ij}^2}{(a - 1)(b - 1)}\) |
| Erro | \(ab(r - 1)\) | \(\sigma^2\) |
https://www.jstor.org/stable/2528712?seq=15#metadata_info_tab_contents.
O quadro de ANOVA pode ser escrito em termos de matriz
| FV | Matriz de projeção | GL | E(SQ) | E(MS) |
|---|---|---|---|---|
| \(\text{tr}(.)\) | \(\text{tr}(.)\sigma^2 + \beta^\top X^\top (.) X\beta\) | \(\sigma^2 + \frac{\beta^\top X^\top (.) X\beta}{\text{tr}(.)}\) | ||
| A | \(H_{\mu:\tau} - H_{\mu}\) | |||
| B | \(H_{\mu:\theta} - H_{\mu:\tau}\) | |||
| AB | \(H_{\mu:\gamma} - H_{\mu:\theta}\) | |||
| Erro | \(I - H_{\mu:\gamma}\) | \(\sigma^2\) | ||
# Quadro de análise de variância.
anova(m0)## Analysis of Variance Table
##
## Response: tv
## Df Sum Sq Mean Sq F value Pr(>F)
## mate 2 10684 5341.9 7.9114 0.001976 **
## temp 2 39119 19559.4 28.9677 1.909e-07 ***
## mate:temp 4 9614 2403.4 3.5595 0.018611 *
## Residuals 27 18231 675.2
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Por meio de expressões com somas de quadrados, que foram aprendidas e constantemente usadas em CE 213 · Planejamento de Experimentos I, pode-se obter o quadro de análise de variância para experimentos como este que é balanceado e de efeitos ortogonais.
As expressões relevantes são \[ \begin{align*} C &= \frac{y_{...}^2}{abr}\\ SS_\text{Total} &= \sum_{i} \sum_{j} \sum_{k} y_{ijk}^2 - C\\ SS_A &= \frac{1}{br} \sum_i y_{i..}^2 - C\\ SS_B &= \frac{1}{ar} \sum_j y_{.j.}^2 - C\\ SS_{A\cap B} &= \frac{1}{r} \sum_i \sum_j y_{ij.}^2 - C\\ SS_{AB} &= SS_{A\cap B} - SS_A - SS_B\\ SS_{\text{Erro}} &= SS_\text{Total} - SS_{AB} - SS_B - SS_A. \end{align*} \]
A notação de ponto no subíndice indica total sob todas as observações, ou seja, \(y_{i..} = \sum_j \sum_k y_{ijk}\).
# Média dos totais ao quadrado.
squared_mean <- function(y) sum(y)^2/length(y)
# Resultados das somas de quadrados.
C <- aggregate(tv ~ 1, data = tb, squared_mean)$tv
SS_A <- sum(aggregate(tv ~ mate, data = tb, squared_mean)$tv) - C
SS_B <- sum(aggregate(tv ~ temp, data = tb, squared_mean)$tv) - C
SS_AiB <- sum(aggregate(tv ~ mate:temp, data = tb, squared_mean)$tv) - C
SS_AB <- SS_AiB - SS_A - SS_B
SS_Total <- sum(y^2) - C
SS_Erro <- SS_Total - SS_A - SS_B - SS_AB
# Somas de quadrados.
rbind(SS_A, SS_B, SS_AB, SS_Erro)## [,1]
## SS_A 10683.722
## SS_B 39118.722
## SS_AB 9613.778
## SS_Erro 18230.750Apesar das expressões baseadas em somas de quadrados serem muito úteis, elas não são apropriadas para experimentos nos quais não se tem ortogonalidade entre os efeitos, o que pode acontecer por perda de combinações experimentais, perda unidades experimentais, inclusão de covariáveis de níveis não controlados e uso de confundimento, por exemplo. Para lidar com essas situações pode-se obter as somas de quadrados com operações matriciais baseadas em matrizes de projeção.
Na realidade, as expressões com somas de quadrados são de fato a simplificação algébrica das equivalentes expressões matriciais.
A vantagem é que com o uso das matrizes de projeção é possível contemplar a interpretação geométrica do método de mínimos quadrados, além de permitir acomodar experimentos de estrutura irregular.
As somas de quadrados são o comprimento do vetor resultante da projeção do vetor das observações em um subespaço linear definido pelas colunas da matriz do modelo. A matriz de projeção é obtida por meio da matriz de delineamento ou matriz do modelo \[ H = X (X^\top X)^{-1} X^\top. \]
Considere que a matriz do modelo foi particinada criando uma sequência de matrizes em que a seguinte tem o conjunto de colunas que acomoda um termo não contido na precedente. Colocando de outra forma, essa sequência de matrizes corresponde aos modelos \[ \begin{aligned} \mu_{ij} = \mu \quad \Rightarrow &\quad X_{\mu} \\ \mu_{ij} = \mu + \tau_i \quad \Rightarrow &\quad X_{\mu:\tau} \\ \mu_{ij} = \mu + \tau_i + \theta_j \quad \Rightarrow &\quad X_{\mu:\theta} \\ \mu_{ij} = \mu + \tau_i + \theta_j + \gamma_{ij} \quad \Rightarrow &\quad X_{\mu:\gamma}, \end{aligned} \] portanto, o operador \(:\) no subíndice indica o intervalo de parâmetros cujas colunas estão na matriz.
Será útil para demonstrações as matrizes correspondentes aos modelos \[\begin{aligned} \mu_{ij} = \mu + \tau_i \quad \Rightarrow &\quad X_{\mu,\tau} \\ \mu_{ij} = \mu + \theta_j \quad \Rightarrow &\quad X_{\mu,\theta} \\ \mu_{ij} = \mu + \gamma_{ij} \quad \Rightarrow &\quad X_{\mu,\gamma}. \end{aligned}\]Formas quadráticas usando as matrizes de projeção retornam as somas de quadrados. O grau de liberdade corresponde ao traço da matriz usada para obter as somas de quadrados. As matrizes de projeção, mantendo a sequência de modelos, são \[ \begin{aligned} H_{\mu} &= X_{\mu} (X_{\mu}^\top X_{\mu})^{-1} X_{\mu}^\top\\ H_{\mu:\tau} &= X_{\mu:\tau} (X_{\mu:\tau}^\top X_{\mu:\tau})^{-1} X_{\mu:\tau}^\top\\ H_{\mu:\theta} &= X_{\mu:\theta} (X_{\mu:\theta}^\top X_{\mu:\theta})^{-1} X_{\mu:\theta}^\top\\ H_{\mu:\gamma} &= X_{\mu:\gamma} (X_{\mu:\gamma}^\top X_{\mu:\gamma})^{-1} X_{\mu:\gamma}^\top. \end{aligned} \]
Dessa forma, as somas de quadrados são obtidas por \[ \begin{aligned} C &= y^\top H_{\mu} y\\ SS_A &= y^\top (H_{\mu:\tau} - H_{\mu}) y = y^\top (H_{\mu:\tau}) y - y^\top (H_{\mu}) y\\ SS_B &= y^\top (H_{\mu:\theta} - H_{\mu:\tau}) y \\ &= y^\top (H_{\mu,\theta} - H_{\mu}) y \quad \text{ pois }\quad (H_{\mu,\theta} - H_{\mu}) \perp (H_{\mu,\tau} - H_{\mu})\\ SS_{AB} &= y^\top (H_{\mu:\gamma} - H_{\mu:\theta}) y \\ &= y^\top (H_{\mu,\gamma} - H_{\mu}) y \quad \text{ pois }\quad (H_{\mu,\gamma} - H_{\mu}) \perp (H_{\mu,\theta} - H_{\mu})\\ SS_{\text{Erro}} &= y^\top (I - H_{\mu:\gamma}) y. \\ \end{aligned} \]
O código a seguir calcula as somas de quadrados conforme indicado pelas expressões acima.
X <- model.matrix(~mate * temp,
data = tb,
contrasts.arg = list(mate = contr.sum,
temp = contr.sum))
proj <- function(X) {
X %*% solve(crossprod(X), t(X))
}
a <- attr(X, "assign")
a## [1] 0 1 1 2 2 3 3 3 3I <- diag(length(y))
H0 <- proj(X[, a <= 0])
H01 <- proj(X[, a <= 1])
H02 <- proj(X[, a <= 2])
H03 <- proj(X[, a <= 3])
# Somas de quadrados sequênciais.
t(y) %*% (H0) %*% y # C: RSS(~1) - RSS(~0).## [,1]
## [1,] 400900t(y) %*% (H01 - H0) %*% y # SS_A: RSS(~A) - RSS(~1).## [,1]
## [1,] 10683.72t(y) %*% (H02 - H01) %*% y # SS_B: RSS(~A + B) - RSS(~A).## [,1]
## [1,] 39118.72t(y) %*% (H03 - H02) %*% y # SS_AB: RSS(~A * B) - RSS(~A + B).## [,1]
## [1,] 9613.778t(y) %*% (I - H03) %*% y # SS_Erro.## [,1]
## [1,] 18230.75anova(m0)## Analysis of Variance Table
##
## Response: tv
## Df Sum Sq Mean Sq F value Pr(>F)
## mate 2 10684 5341.9 7.9114 0.001976 **
## temp 2 39119 19559.4 28.9677 1.909e-07 ***
## mate:temp 4 9614 2403.4 3.5595 0.018611 *
## Residuals 27 18231 675.2
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1# Como os efeitos são ortogonais, sequêncial e um termo por vez dá
# igual.
H1 <- proj(X[, a %in% c(0, 1)])
H2 <- proj(X[, a %in% c(0, 2)])
H3 <- proj(X[, a %in% c(0, 3)])
# Somas de quadrados de um termo de cada vez.
# ATTENTION: Para funcionar tem que usar restrições lineares ortogonais,
# i.e. `contr.sum`, `contr.helmert` ou `contr.poly`.
t(y) %*% (H1 - H0) %*% y # SS_A: RSS(~A) - RSS(~1).## [,1]
## [1,] 10683.72t(y) %*% (H2 - H0) %*% y # SS_B: RSS(~B) - RSS(~1).## [,1]
## [1,] 39118.72t(y) %*% (H3 - H0) %*% y # SS_AB: RSS(~A:B) - RSS(~1).## [,1]
## [1,] 9613.778# Mostra que as projeções são ortogonais.
all(round((H1 - H0) %*% (H2 - H0), digits = 4) == 0)## [1] TRUEtrace <- function(H) {
sum(diag(H))
}
# Graus de liberdade.
trace(H0)## [1] 1trace(H01 - H0)## [1] 2trace(H02 - H01)## [1] 2trace(H03 - H02)## [1] 4trace(I - H03)## [1] 271.1.4 Estudo da interação
Quando ocorre interação é porque a predição (média) não é função apenas dos efeitos principais dos fatores. Colocando de outra forma, a interação dupla entre os fatores material e temperatura indica que a diferência em tempo médio de vida da bateria entre dois níveis de temperatura depende do nível de material. O oposto também é verdadeiro, as diferenças entre material mudam com o nível de temperatura.
O fragmento abaixo usa o pacote emmeans (estimated marginal means) para obter as médias de duração de bateria para cada ponto experimental.
# Médias marginais ajustadas = valores preditos para cada ponto
# experimental.
emm <- emmeans(m0, specs = ~temp | mate)
emm## mate = 1:
## temp emmean SE df lower.CL upper.CL
## 15 134.8 13 27 108.1 161.4
## 70 57.2 13 27 30.6 83.9
## 125 57.5 13 27 30.8 84.2
##
## mate = 2:
## temp emmean SE df lower.CL upper.CL
## 15 155.8 13 27 129.1 182.4
## 70 119.8 13 27 93.1 146.4
## 125 49.5 13 27 22.8 76.2
##
## mate = 3:
## temp emmean SE df lower.CL upper.CL
## 15 144.0 13 27 117.3 170.7
## 70 145.8 13 27 119.1 172.4
## 125 85.5 13 27 58.8 112.2
##
## Confidence level used: 0.95attr(emm, "grid")## temp mate .wgt.
## 1 15 1 4
## 2 70 1 4
## 3 125 1 4
## 4 15 2 4
## 5 70 2 4
## 6 125 2 4
## 7 15 3 4
## 8 70 3 4
## 9 125 3 4unname(attr(emm, "linfct"))## [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9]
## [1,] 1 0 0 0 0 0 0 0 0
## [2,] 1 0 0 1 0 0 0 0 0
## [3,] 1 0 0 0 1 0 0 0 0
## [4,] 1 1 0 0 0 0 0 0 0
## [5,] 1 1 0 1 0 1 0 0 0
## [6,] 1 1 0 0 1 0 0 1 0
## [7,] 1 0 1 0 0 0 0 0 0
## [8,] 1 0 1 1 0 0 1 0 0
## [9,] 1 0 1 0 1 0 0 0 1# Constrastes entre níveis de temperatura para cada nível de material.
contrast(emm, method = "pairwise")## mate = 1:
## contrast estimate SE df t.ratio p.value
## 15 - 70 77.50 18.4 27 4.218 0.0007
## 15 - 125 77.25 18.4 27 4.204 0.0007
## 70 - 125 -0.25 18.4 27 -0.014 0.9999
##
## mate = 2:
## contrast estimate SE df t.ratio p.value
## 15 - 70 36.00 18.4 27 1.959 0.1419
## 15 - 125 106.25 18.4 27 5.783 <.0001
## 70 - 125 70.25 18.4 27 3.823 0.0020
##
## mate = 3:
## contrast estimate SE df t.ratio p.value
## 15 - 70 -1.75 18.4 27 -0.095 0.9950
## 15 - 125 58.50 18.4 27 3.184 0.0099
## 70 - 125 60.25 18.4 27 3.279 0.0078
##
## P value adjustment: tukey method for comparing a family of 3 estimatesNo fragmento a seguir são obtidas as médias ajustadas, o seu erro padrão, o contraste entre duas médias e o erro padrão.
# Estimativas das médias ajustadas.
Xu <- unique(model.matrix(m0))
Xu %*% coef(m0)## [,1]
## 1 134.75
## 3 155.75
## 5 144.00
## 13 57.25
## 15 119.75
## 17 145.75
## 25 57.50
## 27 49.50
## 29 85.50# Erro padrão das médias.
sqrt(diag(Xu %*% vcov(m0) %*% t(Xu)))## 1 3 5 13 15 17 25
## 12.99243 12.99243 12.99243 12.99243 12.99243 12.99243 12.99243
## 27 29
## 12.99243 12.99243# O erro padrão é \sqrt{\hat{\sigma}^2/r}.
sqrt((deviance(m0)/df.residual(m0))/4)## [1] 12.99243grid <- unique(m0$model[, all.vars(m0$terms)[-1]])
cbind(grid, "." = "|", unname(Xu))## mate temp . 1 2 3 4 5 6 7 8 9
## 1 1 15 | 1 0 0 0 0 0 0 0 0
## 3 2 15 | 1 1 0 0 0 0 0 0 0
## 5 3 15 | 1 0 1 0 0 0 0 0 0
## 13 1 70 | 1 0 0 1 0 0 0 0 0
## 15 2 70 | 1 1 0 1 0 1 0 0 0
## 17 3 70 | 1 0 1 1 0 0 1 0 0
## 25 1 125 | 1 0 0 0 1 0 0 0 0
## 27 2 125 | 1 1 0 0 1 0 0 1 0
## 29 3 125 | 1 0 1 0 1 0 0 0 1# Contraste `temp@15 - temp@70 | mate@1`.
K <- Xu[1,, drop = FALSE] - Xu[4,, drop = FALSE]
K %*% coef(m0) # Estimativa.## [,1]
## 1 77.5sqrt(diag(K %*% vcov(m0) %*% t(K))) # Erro padrão.## 1
## 18.37407tbm <- as.data.frame(emm)
tbm## temp mate emmean SE df lower.CL upper.CL
## 1 15 1 134.75 12.99243 27 108.09174 161.40826
## 2 70 1 57.25 12.99243 27 30.59174 83.90826
## 3 125 1 57.50 12.99243 27 30.84174 84.15826
## 4 15 2 155.75 12.99243 27 129.09174 182.40826
## 5 70 2 119.75 12.99243 27 93.09174 146.40826
## 6 125 2 49.50 12.99243 27 22.84174 76.15826
## 7 15 3 144.00 12.99243 27 117.34174 170.65826
## 8 70 3 145.75 12.99243 27 119.09174 172.40826
## 9 125 3 85.50 12.99243 27 58.84174 112.15826gg1 <-
ggplot(tbm, aes(x = temp, y = emmean)) +
facet_wrap(facets = ~mate) +
geom_point() +
geom_errorbar(aes(ymin = lower.CL, ymax = upper.CL),
width = 0.05) +
labs(x = "Temperatura (°C)",
y = "Tempo de vida (h)")
gg2 <-
ggplot(tbm, aes(x = mate, y = emmean)) +
facet_wrap(facets = ~temp) +
geom_point() +
geom_errorbar(aes(ymin = lower.CL, ymax = upper.CL),
width = 0.05) +
labs(x = "Material",
y = "Tempo de vida (h)")
gridExtra::grid.arrange(gg1, gg2, ncol = 1)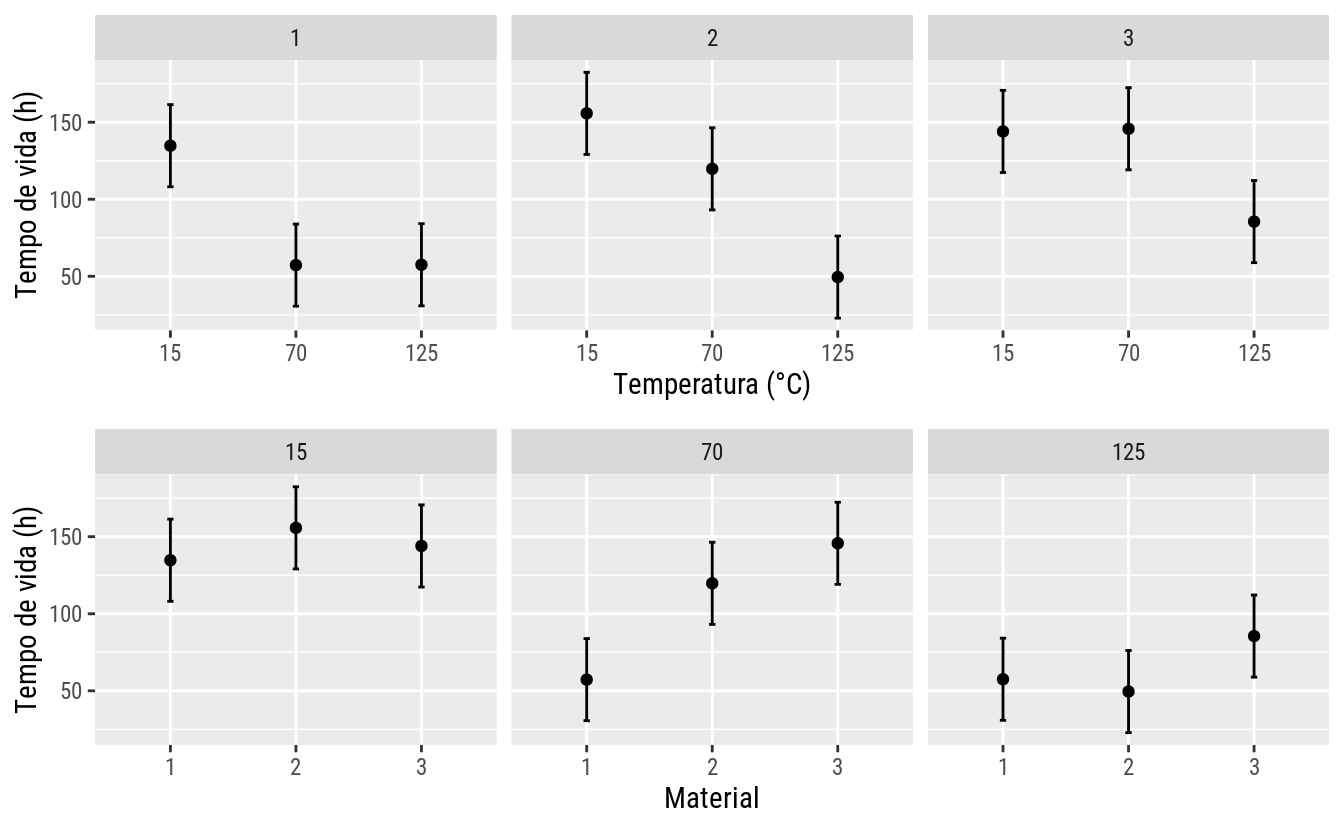
1.2 Fatorial duplo · Soja
Os dados analisados nessa sessão também são de experimento fatorial duplo, no caso um 3 \(\times\) 5 instalado no delineamento de blocos casualizados completos com 5 repetições. Estes dados foram usados no artigo SERAFIM, Milson Evaldo et al. Umidade do solo e doses de potássio na cultura da soja. Rev. Ciênc. Agron., Fortaleza, v. 43, n. 2, p. 222-227, June 2012..
1.2.1 Análise exploratória
A análise exploratória TODO
# Importação do arquivo da web.
url <- "http://leg.ufpr.br/~walmes/data/soja.txt"
soja <- read.table(url, header = TRUE, sep = "\t", dec = ",")# Estrutura do objeto.
str(soja)## 'data.frame': 75 obs. of 10 variables:
## $ potassio: int 0 30 60 120 180 0 30 60 120 180 ...
## $ agua : num 37.5 37.5 37.5 37.5 37.5 50 50 50 50 50 ...
## $ bloco : Factor w/ 5 levels "I","II","III",..: 1 1 1 1 1 1 1 1 1 1 ...
## $ rengrao : num 14.6 21.5 24.6 21.9 28.1 ...
## $ pesograo: num 10.7 13.5 15.8 12.8 14.8 ...
## $ kgrao : num 15.1 17.1 19.1 18.1 19.1 ...
## $ pgrao : num 1.18 0.99 0.82 0.85 0.88 1.05 1.08 0.74 1.01 1.01 ...
## $ ts : int 136 159 156 171 190 140 193 200 208 237 ...
## $ nvi : int 22 2 0 2 0 20 6 6 7 10 ...
## $ nv : int 56 62 66 68 82 63 86 94 86 97 ...# Repetições de cada ponto experimental.
xtabs(~agua + potassio, data = soja)## potassio
## agua 0 30 60 120 180
## 37.5 5 5 5 5 5
## 50 5 5 5 5 5
## 62.5 5 5 5 5 5# Análise exploratória.
gg1 <-
ggplot(data = soja,
mapping = aes(x = potassio,
y = rengrao,
color = factor(agua))) +
geom_point() +
stat_summary(mapping = aes(group = agua),
geom = "line",
fun.y = "mean")
gg2 <-
ggplot(data = soja,
mapping = aes(x = agua,
y = rengrao,
color = factor(potassio))) +
geom_point() +
stat_summary(mapping = aes(group = potassio),
geom = "line",
fun.y = "mean")
gridExtra::grid.arrange(gg1, gg2, ncol = 1)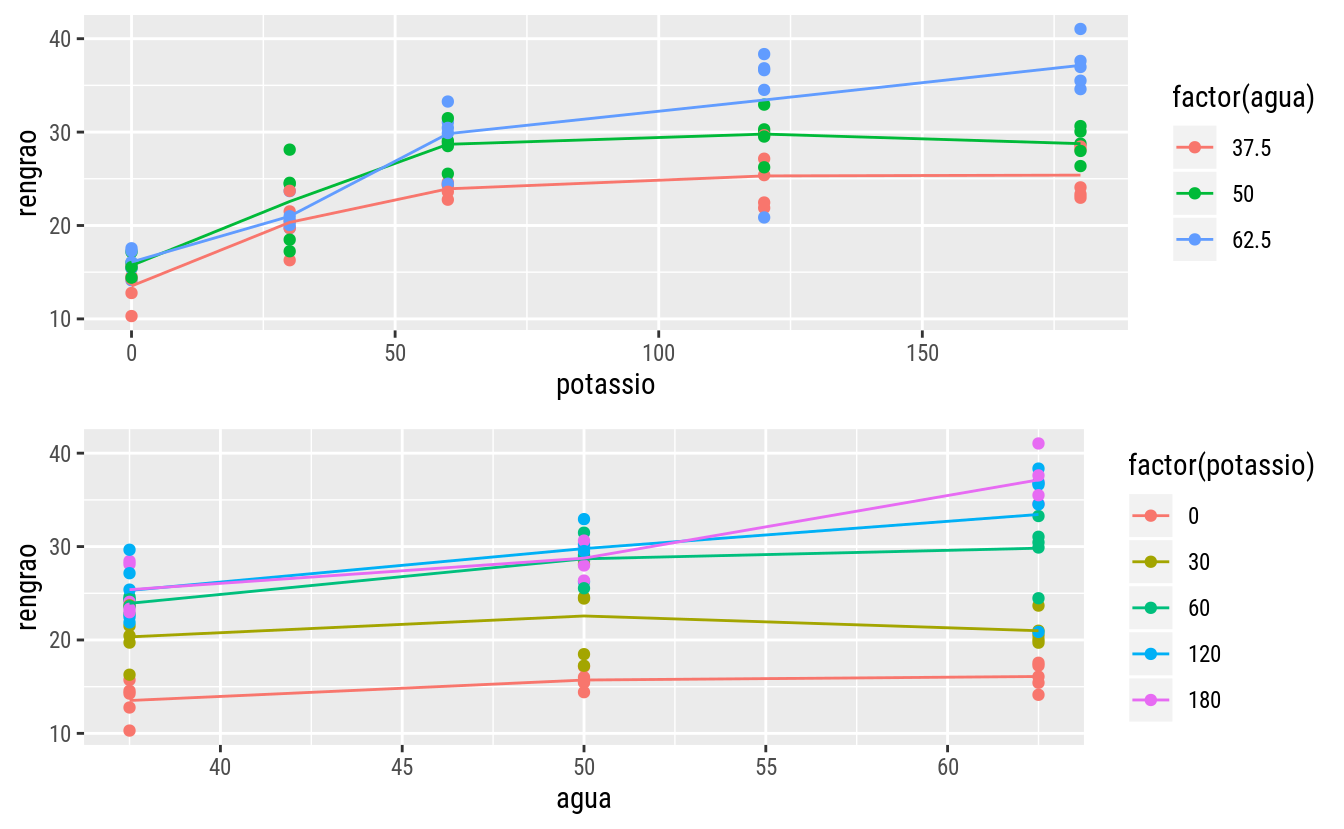
A análise exploratória indica que uma observação do ponto experimental agua = 62.5 & potassio = 120 tem um valor baixo considerando o contexto. Na realidade, foi uma parcela comprometida durante o manuseio ficando apenas com uma ao invés de duas plantas no vaso. As variáveis rengrao, ts, nv e nvi foram então afetadas por isso. Existem 3 alternativas:
- Multiplar o valor observado na parcela por 2 para as variáveis resposta indicadas (extrapolação).
- Remover essa parcela da análise para as variáveis resposta indicadas (perda de informação parcial).
- Conduzir uma análise de variância ponderada para as variáveis resposta indicadas, usando o peso 2 para todas as unidades experimentais com 2 plantas e 1 para esta com uma planta (ponderação).
Dentre as alternativas, a 3 é a mais apropriada e tão fácil de implementar quanto as anteriores. Basta que seja criado o vetor de pesos e usado na especificação do modelo para a função lm() por meio do parâmetro weigths.
soja %>%
filter(agua == 62.5 & potassio == 120) %>%
select(rengrao, ts, nvi, nv)## rengrao ts nvi nv
## 1 38.35 271 0 110
## 2 36.63 240 1 94
## 3 36.83 215 2 89
## 4 34.52 229 0 90
## 5 20.86 128 0 55i <- with(soja, agua == 62.5 & potassio == 120 & bloco == "V")
which(i)## [1] 74soja$n <- 2
soja$n[i] <- 1Para conduzir essa análise, será considerado nessa ocasião que ambos os fatores são qualitativos. Dessa forma, o modelo será um modelo de médias de pontos experimentais. Depois será indicado o correspondente modelo para o das variáveis entrarem como fatores quantitativos.
# Cria cópia dos fatores como qualitativos.
soja <- transform(soja,
Agua = factor(agua),
Potassio = factor(potassio))1.2.2 Especificação e ajuste do modelo
# Ajuste do modelo aos dados.
m0 <- lm(rengrao ~ bloco + Agua * Potassio,
data = soja)
# Diagnóstico do modelo sem ponderação.
par(mfrow = c(2, 2))
plot(m0)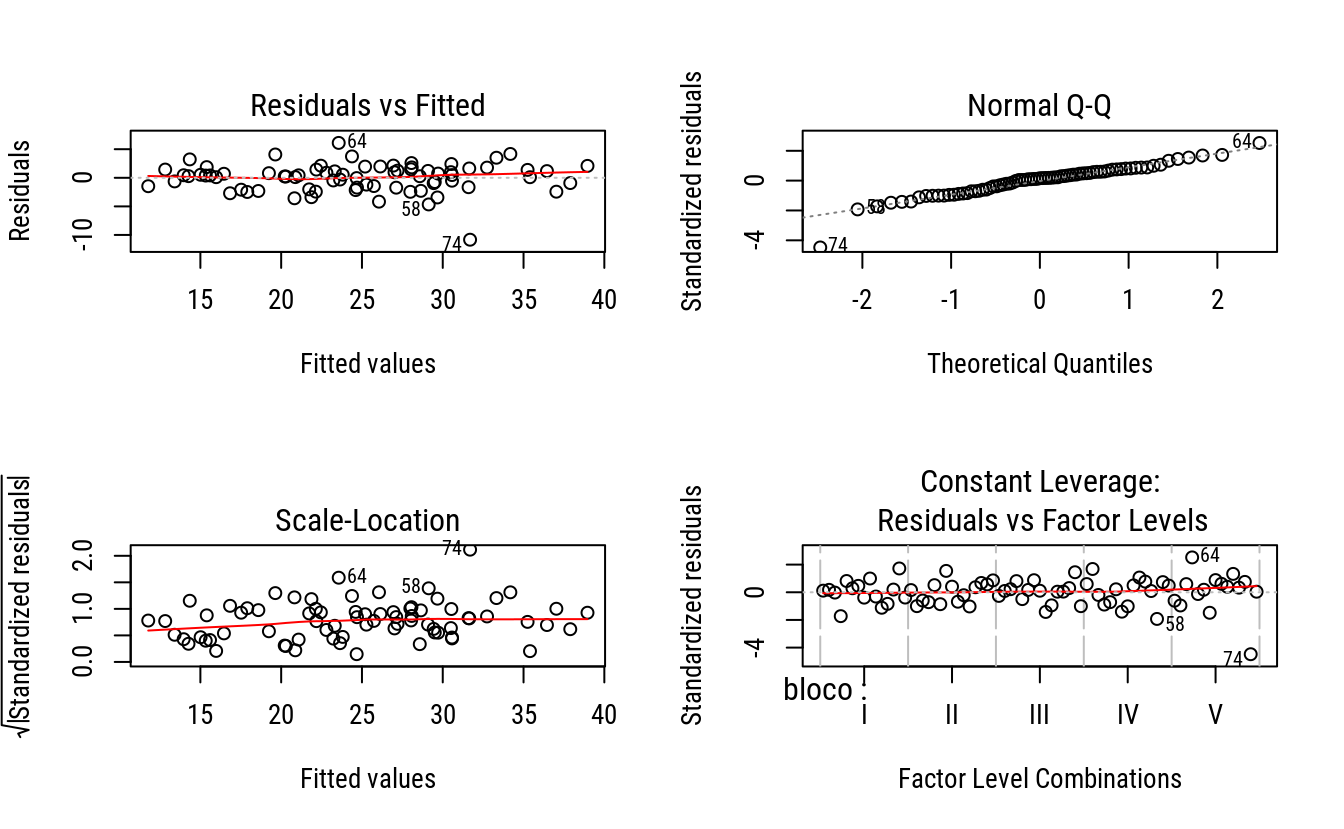
layout(1)
# A variável resposta é a média amostral dentro da unidade experimental.
m1 <- lm(rengrao/n ~ bloco + Agua * Potassio,
data = soja,
weights = n)
# Diagnóstico do modelo com ponderação.
par(mfrow = c(2, 2))
plot(m1)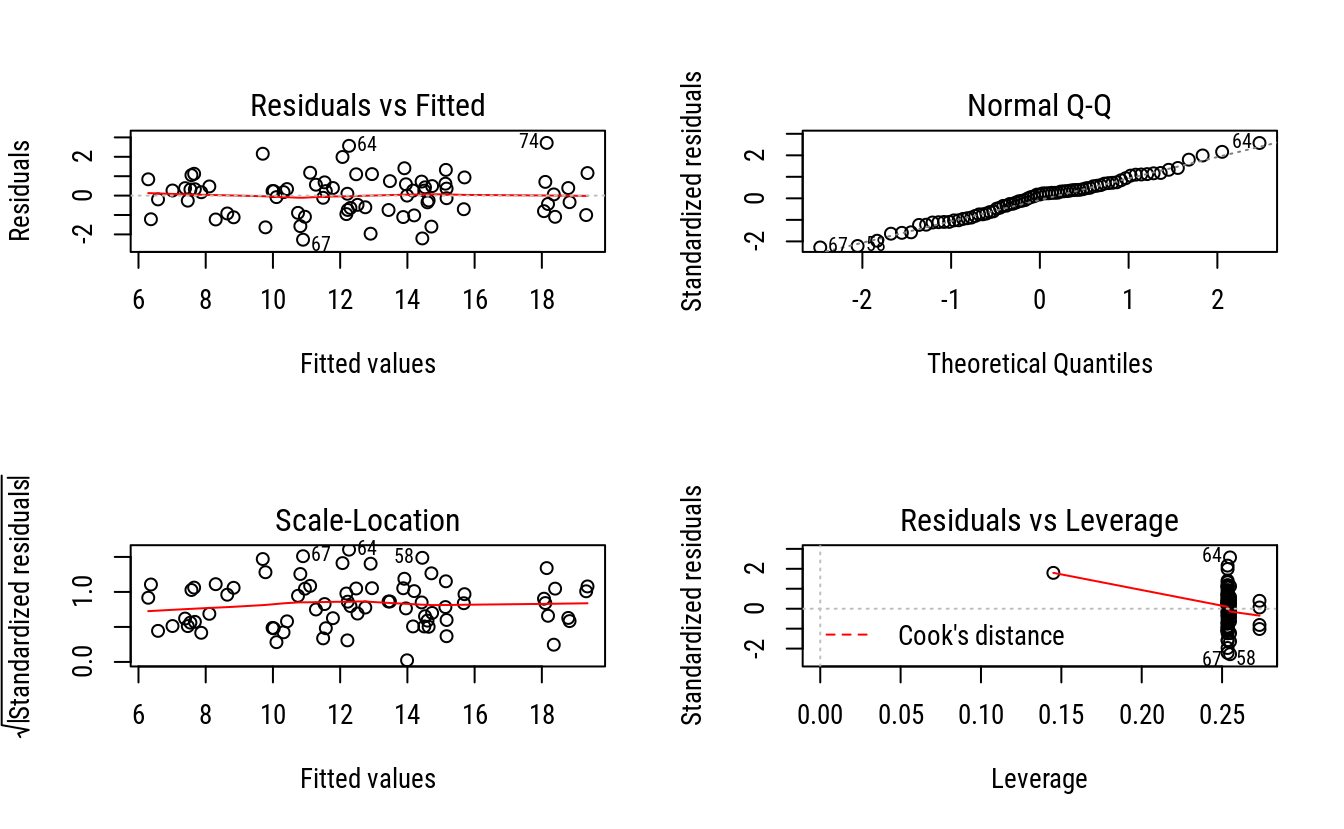
layout(1)1.2.3 O quadro de análise de variância
O quadro de análise de variância aparece a seguir. As contas para obtenção do quadro de ANOVA já foram apresentadas. No entanto, para acomodar os pesos não serão apresentadas as expressões de somatório. Os pesos entram na solução de mínimos quadrados da seguinte forma \[ \hat{\beta} = (X^\top W X)^{-1} (X^\top W y), \] em que \(W\) é uma matriz diagonal contendo os tamanhos amostrais associados ao vetor \(y\) que é de médias amostrais dentro de cada unidade experimental.
# Quadro de análise de variância.
anova(m1)## Analysis of Variance Table
##
## Response: rengrao/n
## Df Sum Sq Mean Sq F value Pr(>F)
## bloco 4 38.10 9.53 3.5649 0.01165 *
## Agua 2 249.43 124.71 46.6765 1.178e-12 ***
## Potassio 4 1331.86 332.96 124.6184 < 2.2e-16 ***
## Agua:Potassio 8 155.44 19.43 7.2722 1.429e-06 ***
## Residuals 56 149.62 2.67
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1O quadro de análise de variância indica que existe interação entre água e potássio. Nesse ponto poderia-se ir para o estudo da interação por meio de comparações múltiplas. No entanto, pode se estudar a interação com um pouco de mais detalhes no próprio quadro de análise de variância por meio de testes de hipótese do efeito de um fator dentro dos níveis dos demais fatores. Essa hipótese é testada pelo teste F do quadro de análise de variância.
Para decompor as somas de quadrados, especificamos um modelo de efeito aninhados. Em termos de número de parâmetros, o modelo de efeito aninhados tem a mesma quantidade do modelo de efeito cruzados. O que muda é a parametrização e é a partir desta que as hipóteses de efeito de um fator dentro de níveis dos outros é testada. Abaixo estão as expressões dos modelos cruzados e aninhados.
\[ \begin{aligned} \text{E}(y_{ij}) &= \mu + \underset{a - 1}{\tau_i} + \underset{b - 1}{\theta_j} + \underset{(a - 1)(b - 1)}{\gamma_{ij}}\\ &= \mu + \underset{a - 1}{\tau_i} + \underset{a(b - 1)}{\delta_{i(j)}} \end{aligned} \]
Nessas expressões, os números abaixo dos parâmetros correspondem a quantidade de parâmetros em cada termo, em que \(a\) e \(b\) são o número de níveis e cada fator. A quantidade de parâmetros é a mesma pois \[ (b - 1) + (a - 1)(b - 1) = a(b - 1). \]
A seguir declara-se o modelo de efeitos aninhados de potássio dentro de água e depois de água dentro de potássio. O teste de hipótese é feito a partição das somas de quadrados do quadro de análise de variância. Para a partição é preciso indicar a posição dos parâmetros que estarão sob teste, ou seja, envolvidos na hipótese nula \[ H_{0i}: \begin{bmatrix} \delta_{i(1)}\\ \vdots\\ \delta_{i(b-1)} \\ \end{bmatrix} = \begin{bmatrix} 0 \\ \vdots \\ 0 \end{bmatrix}, i = 1, \ldots, a. \]
O código deixa bastante deduzível como isso é informado e como interpretar o resultado.
# Modelo de efeitos aninhados.
m2 <- aov(pesograo/n ~ bloco + Agua/Potassio,
data = soja,
weights = n)
coef(m2)## (Intercept) blocoII blocoIII
## 5.55694402 0.47333333 0.08966667
## blocoIV blocoV Agua50
## 0.28566667 0.59661323 0.09700000
## Agua62.5 Agua37.5:Potassio30 Agua50:Potassio30
## -0.07400000 0.66700000 0.12400000
## Agua62.5:Potassio30 Agua37.5:Potassio60 Agua50:Potassio60
## 0.65600000 1.58400000 0.95500000
## Agua62.5:Potassio60 Agua37.5:Potassio120 Agua50:Potassio120
## 1.14400000 1.77400000 1.05300000
## Agua62.5:Potassio120 Agua37.5:Potassio180 Agua50:Potassio180
## 2.91883969 2.37500000 0.28400000
## Agua62.5:Potassio180
## 2.26100000# Disposição das estimativas dos parâmetros.
names(coef(m2)[m2$assign == 3])## [1] "Agua37.5:Potassio30" "Agua50:Potassio30"
## [3] "Agua62.5:Potassio30" "Agua37.5:Potassio60"
## [5] "Agua50:Potassio60" "Agua62.5:Potassio60"
## [7] "Agua37.5:Potassio120" "Agua50:Potassio120"
## [9] "Agua62.5:Potassio120" "Agua37.5:Potassio180"
## [11] "Agua50:Potassio180" "Agua62.5:Potassio180"# Para testar o efeito de potássio em cada nível de água.
Pot_in_Ag <- list("Pot@37.5" = c(1, 4, 7, 10),
"Pot@50.0" = c(2, 5, 8, 11),
"Pot@62.5" = c(3, 6, 9, 12))
summary(m2, split = list("Agua:Potassio" = Pot_in_Ag))## Df Sum Sq Mean Sq F value Pr(>F)
## bloco 4 6.44 1.611 0.780 0.543054
## Agua 2 16.50 8.251 3.993 0.023917 *
## Agua:Potassio 12 98.83 8.236 3.986 0.000189 ***
## Agua:Potassio: Pot@37.5 4 35.50 8.874 4.295 0.004221 **
## Agua:Potassio: Pot@50.0 4 9.49 2.374 1.149 0.343222
## Agua:Potassio: Pot@62.5 4 53.84 13.460 6.515 0.000223 ***
## Residuals 56 115.70 2.066
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1# Modelo de efeitos aninhados.
m2 <- aov(pesograo/n ~ bloco + Potassio/Agua,
data = soja,
weights = n)
coef(m2)## (Intercept) blocoII blocoIII
## 5.55694402 0.47333333 0.08966667
## blocoIV blocoV Potassio30
## 0.28566667 0.59661323 0.66700000
## Potassio60 Potassio120 Potassio180
## 1.58400000 1.77400000 2.37500000
## Potassio0:Agua50 Potassio30:Agua50 Potassio60:Agua50
## 0.09700000 -0.44600000 -0.53200000
## Potassio120:Agua50 Potassio180:Agua50 Potassio0:Agua62.5
## -0.62400000 -1.99400000 -0.07400000
## Potassio30:Agua62.5 Potassio60:Agua62.5 Potassio120:Agua62.5
## -0.08500000 -0.51400000 1.07083969
## Potassio180:Agua62.5
## -0.18800000# Disposição das estimativas dos parâmetros.
names(coef(m2)[m2$assign == 3])## [1] "Potassio0:Agua50" "Potassio30:Agua50"
## [3] "Potassio60:Agua50" "Potassio120:Agua50"
## [5] "Potassio180:Agua50" "Potassio0:Agua62.5"
## [7] "Potassio30:Agua62.5" "Potassio60:Agua62.5"
## [9] "Potassio120:Agua62.5" "Potassio180:Agua62.5"# Para testar o efeito de água em cada nível de potássio.
Ag_in_Pot <- list("Agua@0" = c(1, 6),
"Agua@30" = c(2, 7),
"Agua@60" = c(3, 8),
"Agua@120" = c(4, 9),
"Agua@180" = c(5,10))
summary(m2, split = list("Potassio:Agua" = Ag_in_Pot))## Df Sum Sq Mean Sq F value Pr(>F)
## bloco 4 6.44 1.611 0.780 0.54305
## Potassio 4 74.20 18.551 8.979 1.13e-05 ***
## Potassio:Agua 10 41.13 4.113 1.991 0.05171 .
## Potassio:Agua: Agua@0 2 0.15 0.074 0.036 0.96505
## Potassio:Agua: Agua@30 2 1.12 0.561 0.271 0.76329
## Potassio:Agua: Agua@60 2 1.83 0.913 0.442 0.64516
## Potassio:Agua: Agua@120 2 13.79 6.896 3.338 0.04272 *
## Potassio:Agua: Agua@180 2 24.24 12.122 5.867 0.00486 **
## Residuals 56 115.70 2.066
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 11.2.4 Estudo da interação
emm_pot_ag <- emmeans(m1, specs = ~Potassio | Agua)
emm_pot_ag## Agua = 37.5:
## Potassio emmean SE df lower.CL upper.CL
## 0 6.76 0.517 56 5.72 7.80
## 30 10.17 0.517 56 9.13 11.20
## 60 11.96 0.517 56 10.93 13.00
## 120 12.65 0.517 56 11.62 13.69
## 180 12.70 0.517 56 11.66 13.73
##
## Agua = 50:
## Potassio emmean SE df lower.CL upper.CL
## 0 7.86 0.517 56 6.82 8.89
## 30 11.29 0.517 56 10.25 12.32
## 60 14.35 0.517 56 13.31 15.38
## 120 14.89 0.517 56 13.86 15.93
## 180 14.38 0.517 56 13.34 15.42
##
## Agua = 62.5:
## Potassio emmean SE df lower.CL upper.CL
## 0 8.04 0.517 56 7.01 9.08
## 30 10.49 0.517 56 9.46 11.53
## 60 14.91 0.517 56 13.88 15.95
## 120 18.53 0.546 56 17.44 19.63
## 180 18.57 0.517 56 17.54 19.61
##
## Results are averaged over the levels of: bloco
## Confidence level used: 0.95contrast(emm_pot_ag, method = "pairwise")## Agua = 37.5:
## contrast estimate SE df t.ratio p.value
## 0 - 30 -3.4070 0.731 56 -4.661 0.0002
## 0 - 60 -5.2030 0.731 56 -7.118 <.0001
## 0 - 120 -5.8940 0.731 56 -8.063 <.0001
## 0 - 180 -5.9350 0.731 56 -8.119 <.0001
## 30 - 60 -1.7960 0.731 56 -2.457 0.1155
## 30 - 120 -2.4870 0.731 56 -3.402 0.0105
## 30 - 180 -2.5280 0.731 56 -3.458 0.0089
## 60 - 120 -0.6910 0.731 56 -0.945 0.8779
## 60 - 180 -0.7320 0.731 56 -1.001 0.8536
## 120 - 180 -0.0410 0.731 56 -0.056 1.0000
##
## Agua = 50:
## contrast estimate SE df t.ratio p.value
## 0 - 30 -3.4290 0.731 56 -4.691 0.0002
## 0 - 60 -6.4900 0.731 56 -8.878 <.0001
## 0 - 120 -7.0370 0.731 56 -9.626 <.0001
## 0 - 180 -6.5240 0.731 56 -8.925 <.0001
## 30 - 60 -3.0610 0.731 56 -4.187 0.0009
## 30 - 120 -3.6080 0.731 56 -4.936 0.0001
## 30 - 180 -3.0950 0.731 56 -4.234 0.0008
## 60 - 120 -0.5470 0.731 56 -0.748 0.9440
## 60 - 180 -0.0340 0.731 56 -0.047 1.0000
## 120 - 180 0.5130 0.731 56 0.702 0.9552
##
## Agua = 62.5:
## contrast estimate SE df t.ratio p.value
## 0 - 30 -2.4490 0.731 56 -3.350 0.0121
## 0 - 60 -6.8690 0.731 56 -9.397 <.0001
## 0 - 120 -10.4884 0.752 56 -13.954 <.0001
## 0 - 180 -10.5280 0.731 56 -14.402 <.0001
## 30 - 60 -4.4200 0.731 56 -6.046 <.0001
## 30 - 120 -8.0394 0.752 56 -10.696 <.0001
## 30 - 180 -8.0790 0.731 56 -11.052 <.0001
## 60 - 120 -3.6194 0.752 56 -4.815 0.0001
## 60 - 180 -3.6590 0.731 56 -5.005 0.0001
## 120 - 180 -0.0396 0.752 56 -0.053 1.0000
##
## Results are averaged over the levels of: bloco
## P value adjustment: tukey method for comparing a family of 5 estimatesemm_ag_pot <- emmeans(m1, specs = ~Agua | Potassio)
emm_ag_pot## Potassio = 0:
## Agua emmean SE df lower.CL upper.CL
## 37.5 6.76 0.517 56 5.72 7.80
## 50 7.86 0.517 56 6.82 8.89
## 62.5 8.04 0.517 56 7.01 9.08
##
## Potassio = 30:
## Agua emmean SE df lower.CL upper.CL
## 37.5 10.17 0.517 56 9.13 11.20
## 50 11.29 0.517 56 10.25 12.32
## 62.5 10.49 0.517 56 9.46 11.53
##
## Potassio = 60:
## Agua emmean SE df lower.CL upper.CL
## 37.5 11.96 0.517 56 10.93 13.00
## 50 14.35 0.517 56 13.31 15.38
## 62.5 14.91 0.517 56 13.88 15.95
##
## Potassio = 120:
## Agua emmean SE df lower.CL upper.CL
## 37.5 12.65 0.517 56 11.62 13.69
## 50 14.89 0.517 56 13.86 15.93
## 62.5 18.53 0.546 56 17.44 19.63
##
## Potassio = 180:
## Agua emmean SE df lower.CL upper.CL
## 37.5 12.70 0.517 56 11.66 13.73
## 50 14.38 0.517 56 13.34 15.42
## 62.5 18.57 0.517 56 17.54 19.61
##
## Results are averaged over the levels of: bloco
## Confidence level used: 0.95contrast(emm_ag_pot, method = "pairwise")## Potassio = 0:
## contrast estimate SE df t.ratio p.value
## 37.5 - 50 -1.096 0.731 56 -1.499 0.2990
## 37.5 - 62.5 -1.285 0.731 56 -1.758 0.1932
## 50 - 62.5 -0.189 0.731 56 -0.259 0.9638
##
## Potassio = 30:
## contrast estimate SE df t.ratio p.value
## 37.5 - 50 -1.118 0.731 56 -1.529 0.2851
## 37.5 - 62.5 -0.327 0.731 56 -0.447 0.8958
## 50 - 62.5 0.791 0.731 56 1.082 0.5291
##
## Potassio = 60:
## contrast estimate SE df t.ratio p.value
## 37.5 - 50 -2.383 0.731 56 -3.260 0.0053
## 37.5 - 62.5 -2.951 0.731 56 -4.037 0.0005
## 50 - 62.5 -0.568 0.731 56 -0.777 0.7186
##
## Potassio = 120:
## contrast estimate SE df t.ratio p.value
## 37.5 - 50 -2.239 0.731 56 -3.063 0.0093
## 37.5 - 62.5 -5.879 0.752 56 -7.822 <.0001
## 50 - 62.5 -3.640 0.752 56 -4.843 <.0001
##
## Potassio = 180:
## contrast estimate SE df t.ratio p.value
## 37.5 - 50 -1.685 0.731 56 -2.305 0.0633
## 37.5 - 62.5 -5.878 0.731 56 -8.041 <.0001
## 50 - 62.5 -4.193 0.731 56 -5.736 <.0001
##
## Results are averaged over the levels of: bloco
## P value adjustment: tukey method for comparing a family of 3 estimatesgg1 <-
ggplot(as.data.frame(emm_pot_ag),
mapping = aes(x = Potassio, y = emmean, group = 1)) +
facet_wrap(facets = ~Agua, nrow = 1) +
geom_point() +
geom_line() +
geom_errorbar(aes(ymin = lower.CL, ymax = upper.CL),
width = 0.1) +
labs(x = "Potássio",
y = "Rendimento de grãos")
gg2 <-
ggplot(as.data.frame(emm_ag_pot),
mapping = aes(x = Agua, y = emmean, group = 1)) +
facet_wrap(facets = ~Potassio, nrow = 1) +
geom_point() +
geom_line() +
geom_errorbar(aes(ymin = lower.CL, ymax = upper.CL),
width = 0.1) +
labs(x = "Água",
y = "Rendimento de grãos")
gridExtra::grid.arrange(gg1, gg2, ncol = 1)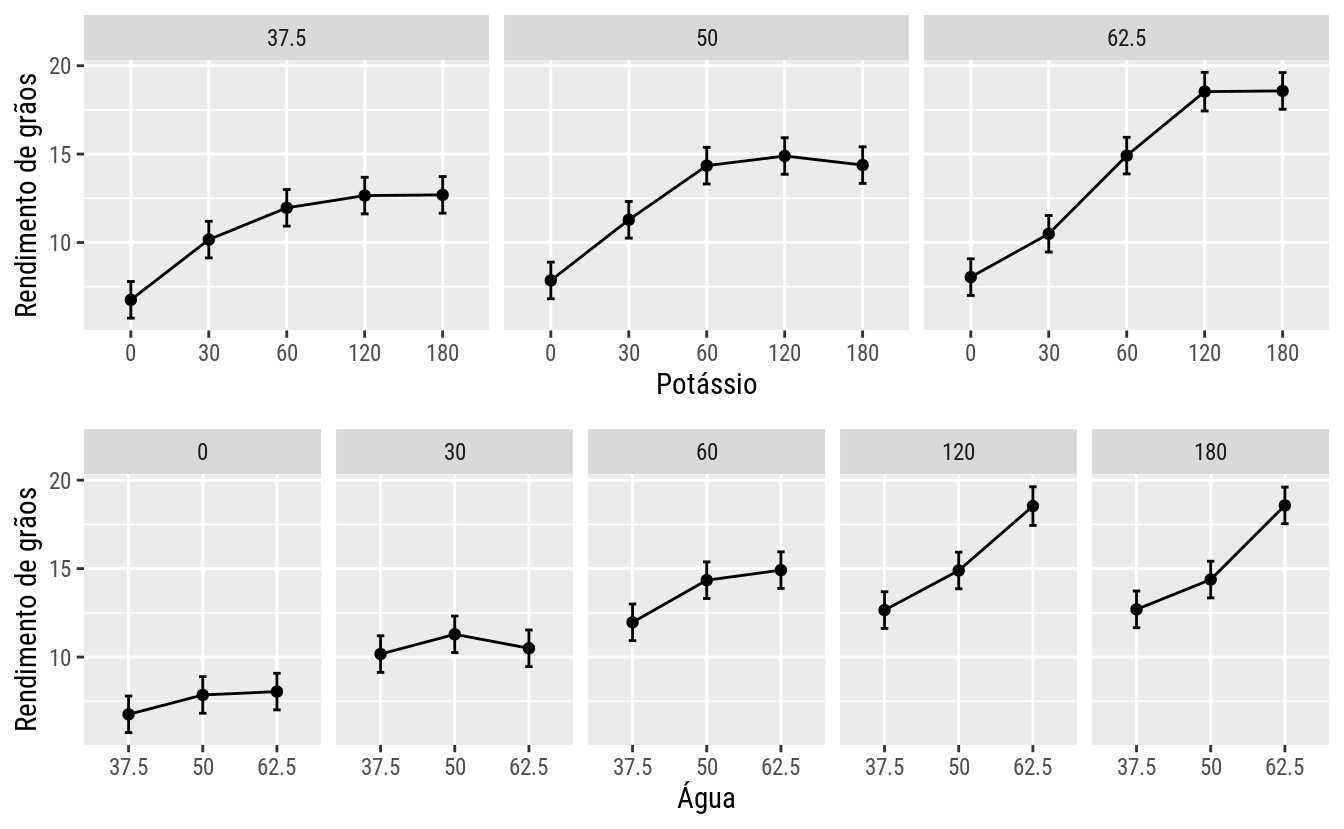
Fica evidente pelos resultados que acomodar o efeito, principalmente de potássio, por uma função numérica dos níveis pode ser mais interessante que considerar como variável qualitativa. Isso será feito em outros momentos durante o curso. No entanto, pode-se adiantar que, dado a trajetória das médias que o acomodar o efeito de potássio por um polinômio de 3º grau e o efeito de água com um de 2º seja suficiente. Dessa forma, o modelo seria \[ \begin{aligned} \text{E}(y_{ij}) &= \mu \\ &+ \tau_1 \cdot \text{ag} + \tau_2 \cdot \text{ag}^2 \\ &+ \theta_1 \cdot \text{pt} + \theta_2 \cdot \text{pt}^2 + \theta_3 \cdot \text{pt}^3\\ &+ \gamma_{11} \cdot \text{ag} \cdot\text{pt} + \gamma_{21} \cdot \text{ag}^2\cdot\text{pt}\\ &+ \gamma_{12} \cdot \text{ag} \cdot\text{pt}^2 + \gamma_{22} \cdot \text{ag}^2\cdot\text{pt}^2\\ &+ \gamma_{13} \cdot \text{ag} \cdot\text{pt}^3 + \gamma_{23} \cdot \text{ag}^2\cdot\text{pt}^3.\\ \end{aligned} \]
O termo que representa o efeito de blocos foi omitido por simplicidade.
1.3 Fatorial triplo · Desvio de enchimento
Para exemplificar a análise do experimento fatorial triplo, será considerado os dados em MONTGOMERY (2008). O contexto do experimento está descrito a seguir.
Um fabricante de refrigerante está interessado em obter volumes de enchimento mais uniformes nas garrafas produzidas por seu processo de fabricação. A máquina de envase teoricamente preenche cada garrafa com o volume alvo correta, mas, na prática, há variação em torno desse alvo, e o fabricante gostaria de entender melhor as fontes dessa variabilidade e, eventualmente, reduzi-las. O engenheiro de processo pode controlar três variáveis durante o processo de enchimento: a porcentagem de carbonatação (A), a pressão operacional no enchimento (B) e as garrafas produzidas por minuto ou a velocidade da linha (C). A pressão e a velocidade são fáceis de controlar, mas a porcentagem de carbonatação é mais difícil de controlar durante a fabricação real porque varia com a temperatura do produto. No entanto, para fins de um experimento, o engenheiro pode controlar a carbonatação em três níveis: 10, 12 e 14 por cento. Ela escolheu dois níveis de pressão (25 e 30 psi) e dois níveis de velocidade de linha (200 e 250 bpm). Ele decidiu executar duas réplicas de um planejamento fatorial nesses três fatores, com todas as 24 tiradas em ordem aleatória. A variável de resposta observada é o desvio médio da altura de enchimento alvo observada em uma corrida de produção de garrafas em cada conjunto de condições. Os dados que resultaram deste experimento são recriados no código abaixo. Desvios positivos são volumes de preenchimento acima do alvo, enquanto desvios negativos são volumes de preenchimento abaixo do alvo.
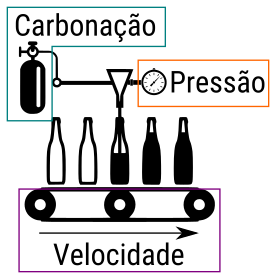
Figura 1.1: Ilustração do processo de enchimento das garrafas indicando os fatores que influenciam o volume de enchimento que estão sob investigação: carbonação, pressão e velocidade.
1.3.1 Análise exploratória
Os gráficos a seguir tem a finalidade de
- Inspecionar a variável resposta em relação a valores atípicos.
- Antecipar a existência de efeito principal dos fatores.
- Antecipar a existência de interações entre os fatores.
# Recria os dados.
da <- data.frame(carb = rep(rep(c(10, 12, 14), each = 2), times = 4),
pres = rep(c(25, 30), each = 12),
velo = rep(c(200, 250, 200, 250), each = 6))
da$dsv <- c(-3, -1, 0, 1, 5, 4,
-1, 0, 2, 1, 7, 6,
-1, 0, 2, 3, 7, 9,
1, 1, 6, 5, 10, 11)
str(da)## 'data.frame': 24 obs. of 4 variables:
## $ carb: num 10 10 12 12 14 14 10 10 12 12 ...
## $ pres: num 25 25 25 25 25 25 25 25 25 25 ...
## $ velo: num 200 200 200 200 200 200 250 250 250 250 ...
## $ dsv : num -3 -1 0 1 5 4 -1 0 2 1 ...# Repetições dos pontos experimentais.
ftable(xtabs(~pres + velo + carb, data = da))## carb 10 12 14
## pres velo
## 25 200 2 2 2
## 250 2 2 2
## 30 200 2 2 2
## 250 2 2 2ggplot(data = da,
mapping = aes(x = carb, y = dsv)) +
facet_grid(facets = pres ~ velo) +
geom_point() +
stat_summary(geom = "line", fun.y = "mean") +
labs(x = "Carbonação (%)", y = "Desvio de enchimento")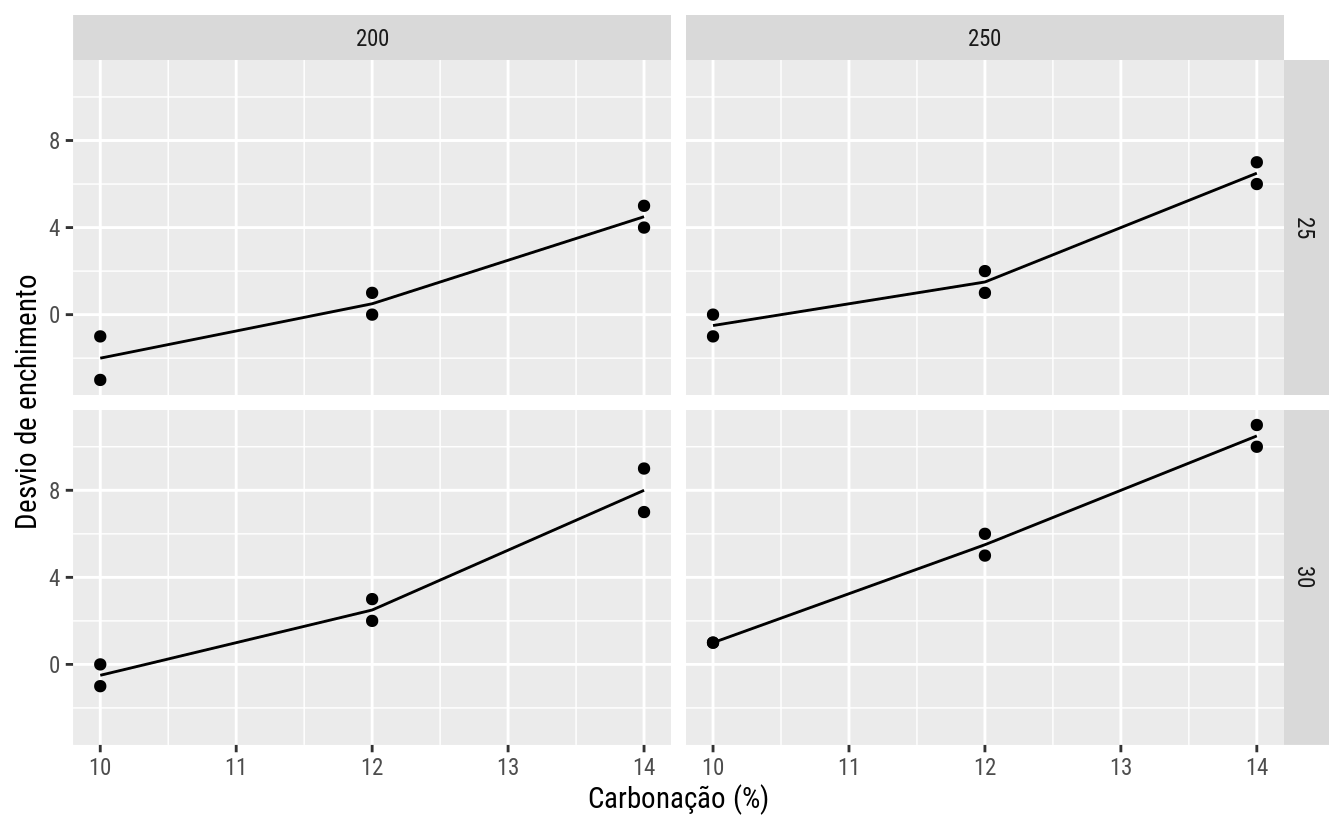
ggplot(data = da,
mapping = aes(x = pres, y = dsv, color = carb)) +
facet_wrap(facets = ~ velo) +
geom_point() +
stat_summary(mapping = aes(group = carb),
geom = "line", fun.y = "mean") +
labs(x = "Pressão", y = "Desvio de enchimento",
color = "Carbonação (%)")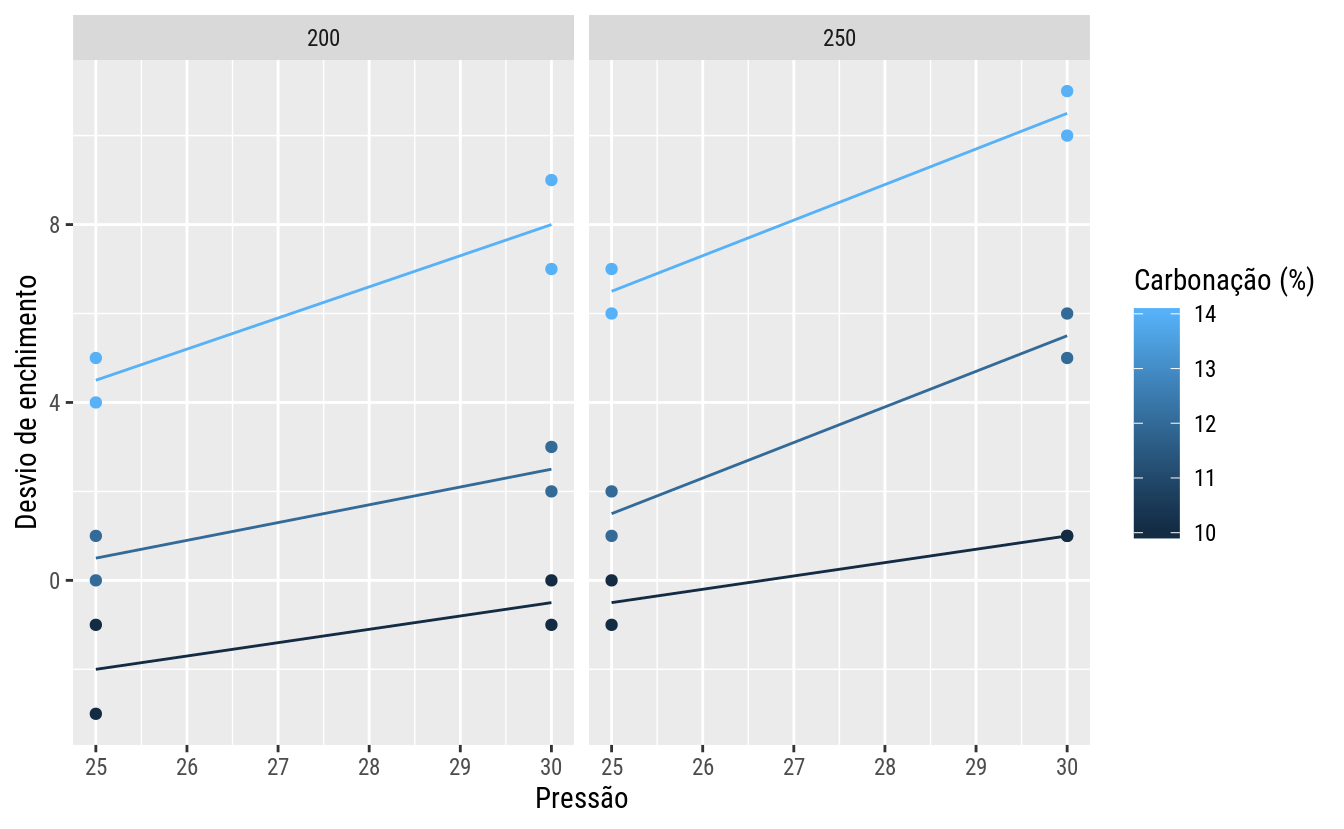
Com base na leitura dos gráficos, conclui-se haver pouca evidência visual para existência de interações. Por outro lado, espera-se que haja efeito principal, especialmente para carbonação.
1.3.2 Especificação e ajuste do modelo
O modelo para o experimento, considerando momentaneamente que todos os fatores são qualitativos, é \[ \begin{aligned} y_{ijkl} &\sim \text{Normal}(\mu_{ijk}, \sigma^2) \\ \mu_{ijk} &= \mu + \alpha_i + \beta_j + \gamma_k + \theta_{ij} + \tau_{ik} + \psi_{jk} + \lambda_{ijk}\\ \sigma^2 &\propto 1, \end{aligned} \] em que \(y_{ijkl}\) é o valor observado para o ponto experimental da carbonação \(i\), pressão \(j\), velocidade \(k\) na repetição \(l\), \(\mu\) é uma constante inerente à todas as observações, \(\alpha_i\) são parâmetros para acomodar o efeito de carbonação, \(\beta_j\) são parâmetros para acomodar o efeito de pressão, \(\gamma_k\) são parâmetros para acomodar o efeito da velocidade. Os demais parâmetros acomodam o efeito de interações duplas e a interação tripla.
Como as variáveis são todas quantitativas, poderia-se, sem prejuízo algum, espeficicar um modelo de efeito para níveis quantitativos usando polinômios. O modelo abaixo é uma alternativa ao anterior que apresentará a mesma qualidade de ajuste visto que é um modelo linear nos parâmetros de mesmo tamanho, ou seja, mesma quantidade de parâmetros. O preditor será \[ \begin{aligned} \mu_{ijk} &= \mu \\ &+ \alpha_1\cdot\text{carb} + \alpha_2\cdot\text{carb}^2 \\ &+ \beta_1\cdot\text{pres} \\ &+ \gamma_1\cdot\text{velo} \\ &+ \theta_{11}\cdot\text{carb}\cdot\text{pres} + \theta_{21}\cdot\text{carb}^2\cdot\text{pres}\\ &+ \tau_{11}\cdot\text{carb}\cdot\text{velo} + \tau_{21}\cdot\text{carb}^2\cdot\text{velo}\\ &+ \psi_{11}\cdot\text{pres}\cdot\text{velo}\\ &+ \lambda_{111}\cdot\text{carb}\cdot\text{pres}\cdot\text{velo} + \lambda_{211}\cdot\text{carb}^2\cdot\text{pres}\cdot\text{velo}\\ \end{aligned} \] em que todos os fatores são descritos por um termo linear e a carbonação que possui 3 níveis, tem o termo quadrático. As interações são produtos dos termos que acomodam os efeitos principais dos três fatores. Manteve-se as mesmas letras gregas, porém, a interpretação dos parâmetros agora é em termos de coeficientes de regressão.
# Cria cópia dos fatores como qualitativos.
da <- transform(da,
Carb = factor(carb),
Pres = factor(pres),
Velo = factor(velo))
# Modelo com interações até 3 grau.
m0 <- lm(dsv ~ Carb * Pres * Velo, data = da)
deviance(m0)## [1] 8.5deviance(lm(dsv ~ (carb + I(carb^2)) * pres * velo, data = da))## [1] 8.5# Diagnóstico sobre os pressupostos.
par(mfrow = c(2, 2))
plot(m0)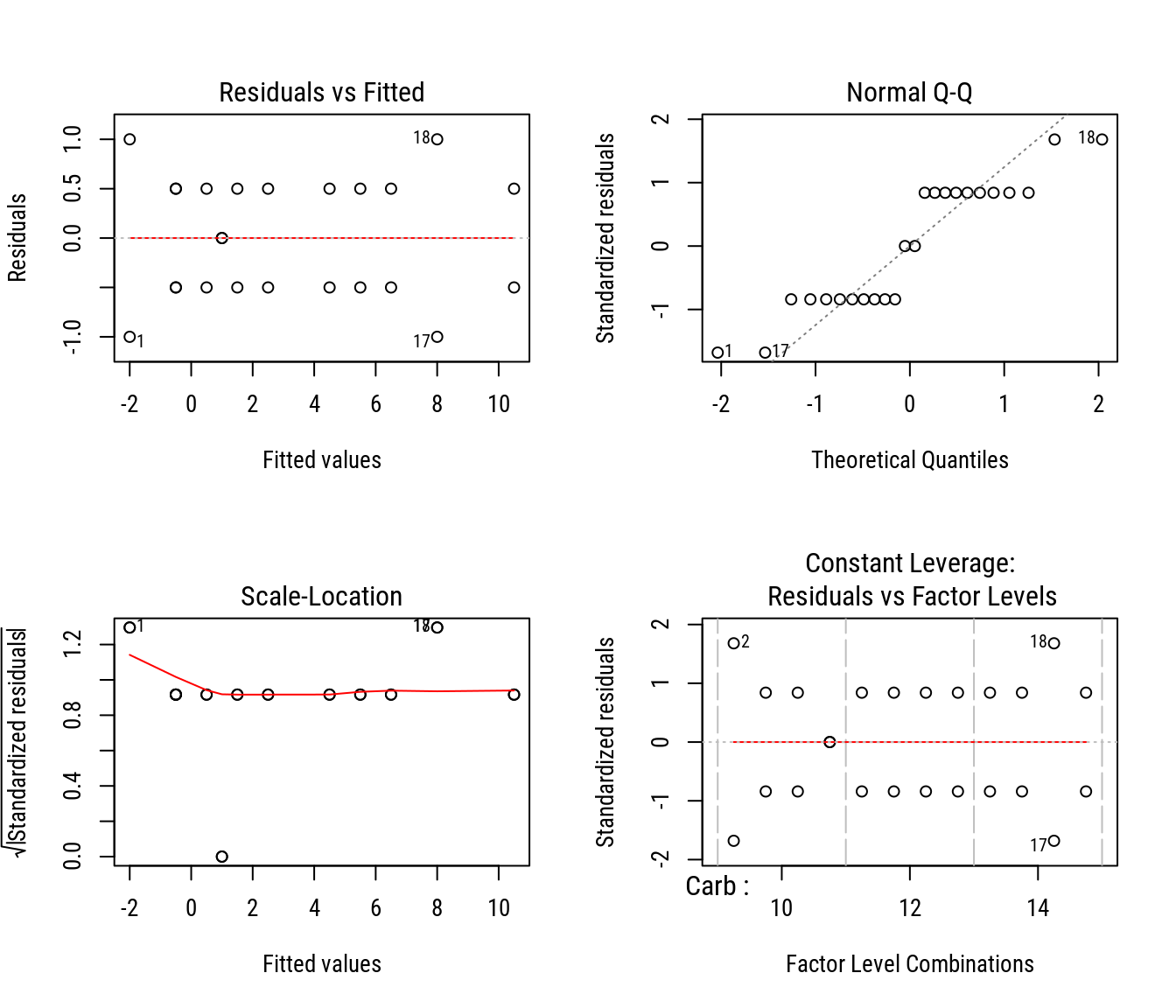
layout(1)
summary(m0)##
## Call:
## lm(formula = dsv ~ Carb * Pres * Velo, data = da)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.0 -0.5 0.0 0.5 1.0
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -2.000e+00 5.951e-01 -3.361 0.00567 **
## Carb12 2.500e+00 8.416e-01 2.970 0.01169 *
## Carb14 6.500e+00 8.416e-01 7.723 5.38e-06 ***
## Pres30 1.500e+00 8.416e-01 1.782 0.10000
## Velo250 1.500e+00 8.416e-01 1.782 0.10000
## Carb12:Pres30 5.000e-01 1.190e+00 0.420 0.68185
## Carb14:Pres30 2.000e+00 1.190e+00 1.680 0.11871
## Carb12:Velo250 -5.000e-01 1.190e+00 -0.420 0.68185
## Carb14:Velo250 5.000e-01 1.190e+00 0.420 0.68185
## Pres30:Velo250 6.345e-16 1.190e+00 0.000 1.00000
## Carb12:Pres30:Velo250 2.000e+00 1.683e+00 1.188 0.25775
## Carb14:Pres30:Velo250 5.000e-01 1.683e+00 0.297 0.77151
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.8416 on 12 degrees of freedom
## Multiple R-squared: 0.9747, Adjusted R-squared: 0.9516
## F-statistic: 42.11 on 11 and 12 DF, p-value: 7.417e-081.3.3 Quadro de análise de variância
O quadro de análise de variância indica não haver efeito da interação tripla. Com isso, na análise das interações duplas não aponta existência de efeito relevante (à 5%).
# Quadro de análise de variância.
anova(m0)## Analysis of Variance Table
##
## Response: dsv
## Df Sum Sq Mean Sq F value Pr(>F)
## Carb 2 252.750 126.375 178.4118 1.186e-09 ***
## Pres 1 45.375 45.375 64.0588 3.742e-06 ***
## Velo 1 22.042 22.042 31.1176 0.0001202 ***
## Carb:Pres 2 5.250 2.625 3.7059 0.0558081 .
## Carb:Velo 2 0.583 0.292 0.4118 0.6714939
## Pres:Velo 1 1.042 1.042 1.4706 0.2485867
## Carb:Pres:Velo 2 1.083 0.542 0.7647 0.4868711
## Residuals 12 8.500 0.708
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1As expressões de somatório para as somas de quadradas apresentadas na sessão anterior podem ser adaptadas para o caso de experimento fatorial triplo. O código abaixo computa as somas de quadrados.
# Média dos totais ao quadrado.
squared_mean <- function(y) sum(y)^2/length(y)
# Resultados das somas de quadrados.
C <- aggregate(dsv ~ 1, data = da, squared_mean)$dsv
SS_A <- sum(aggregate(dsv ~ Carb, data = da, squared_mean)$dsv) - C
SS_B <- sum(aggregate(dsv ~ Pres, data = da, squared_mean)$dsv) - C
SS_C <- sum(aggregate(dsv ~ Velo, data = da, squared_mean)$dsv) - C
SS_AiB <- sum(aggregate(dsv ~ Carb:Pres, data = da,
squared_mean)$dsv) - C
SS_AB <- SS_AiB - SS_A - SS_B
SS_AiC <- sum(aggregate(dsv ~ Carb:Velo, data = da,
squared_mean)$dsv) - C
SS_AC <- SS_AiC - SS_A - SS_C
SS_BiC <- sum(aggregate(dsv ~ Pres:Velo, data = da,
squared_mean)$dsv) - C
SS_BC <- SS_BiC - SS_B - SS_C
SS_AiBiC <- sum(aggregate(dsv ~ Carb:Pres:Velo, data = da,
squared_mean)$dsv) - C
SS_ABC <- SS_AiBiC - SS_A - SS_B - SS_C - SS_AB - SS_AC - SS_BC
SS_Total <- sum(da$dsv^2) - C
SS_Erro <- SS_Total - SS_AiBiC
# Somas de quadrados.
rbind(SS_A, SS_B, SS_AB,
SS_AB, SS_AC, SS_BC,
SS_ABC,
SS_Erro)## [,1]
## SS_A 252.7500000
## SS_B 45.3750000
## SS_AB 5.2500000
## SS_AB 5.2500000
## SS_AC 0.5833333
## SS_BC 1.0416667
## SS_ABC 1.0833333
## SS_Erro 8.50000001.3.4 Médias ajustadas
As médias ajustadas são os valores preditos para cada ponto experimental. Todavia, como não há interação, pode-se obter as médias marginais ajustadas. Elas são médias para os níveis de um fator ponderando ou marginalizando o efeito dos demais fatores. Por exemplo, por meio dos coeficientes estimados do modelo de regressão, a média marginal ajustada para os níveis de carbonação é \[ \begin{aligned} \hat{\mu}_\text{A} &= L_{\text{A}} \hat{\beta} \\ \begin{bmatrix} \hat{\mu}_{1..}\\ \hat{\mu}_{2..}\\ \hat{\mu}_{3..}\\ \end{bmatrix} &= \begin{bmatrix} 1 & 0 & 0 & 1/2 & 1/2 & 0 & 0 & 0 & 0 & 1/4 & 0 & 0 \\ 1 & 1 & 0 & 1/2 & 1/2 & 1/2 & 0 & 1/2 & 0 & 1/4 & 1/4 & 0 \\ 1 & 0 & 1 & 1/2 & 1/2 & 0 & 1/2 & 0 & 1/2 & 1/4 & 0 & 1/4 \\ \end{bmatrix} \begin{bmatrix} \hat{\mu}\\ \hat{\alpha}_2\\ \hat{\alpha}_3\\ \hat{\beta}_2\\ \hat{\gamma}_2\\ \hat{\theta}_{22}\\ \hat{\theta}_{32}\\ \hat{\tau}_{22}\\ \hat{\tau}_{32}\\ \hat{\psi}_{22}\\ \hat{\lambda}_{222}\\ \hat{\lambda}_{322}\\ \end{bmatrix}. \end{aligned} \]
O pacote emmeans permite obter as médias marginais para uma ampla classe de modelos. O pacote constrói a matriz \(L\) conforme uso do argumento specs. A vantagem é que ela considera o tipo de contraste que foi usado para solucionar o problema de mínimos quadrados.
# Médias marginais ajustas para o efeito principal de carbonação.
emm <- emmeans(m0, specs = ~Carb)## NOTE: Results may be misleading due to involvement in interactionsemm## Carb emmean SE df lower.CL upper.CL
## 10 -0.50 0.298 12 -1.15 0.148
## 12 2.50 0.298 12 1.85 3.148
## 14 7.38 0.298 12 6.73 8.023
##
## Results are averaged over the levels of: Pres, Velo
## Confidence level used: 0.95MASS::fractions(attr(emm, "linfct"))## (Intercept) Carb12 Carb14 Pres30 Velo250 Carb12:Pres30
## [1,] 1 0 0 1/2 1/2 0
## [2,] 1 1 0 1/2 1/2 1/2
## [3,] 1 0 1 1/2 1/2 0
## Carb14:Pres30 Carb12:Velo250 Carb14:Velo250 Pres30:Velo250
## [1,] 0 0 0 1/4
## [2,] 0 1/2 0 1/4
## [3,] 1/2 0 1/2 1/4
## Carb12:Pres30:Velo250 Carb14:Pres30:Velo250
## [1,] 0 0
## [2,] 1/4 0
## [3,] 0 1/4attr(emm, "linfct") %*% coef(m0)## [,1]
## [1,] -0.500
## [2,] 2.500
## [3,] 7.375contrast(emm, method = "pairwise")## contrast estimate SE df t.ratio p.value
## 10 - 12 -3.00 0.421 12 -7.129 <.0001
## 10 - 14 -7.88 0.421 12 -18.714 <.0001
## 12 - 14 -4.88 0.421 12 -11.585 <.0001
##
## Results are averaged over the levels of: Pres, Velo
## P value adjustment: tukey method for comparing a family of 3 estimatesAs médias marginais para o efeito de pressão são obtidas com a seguinte função linear das estimativas dos parâmetros \[ \begin{aligned} \hat{\mu}_\text{B} &= L_{\text{B}} \hat{\beta} \\ \begin{bmatrix} \hat{\mu}_{.1.}\\ \hat{\mu}_{.2.}\\ \end{bmatrix} &= \begin{bmatrix} 1 & 1/3 & 1/3 & 0 & 1/2 & 0 & 0 & 1/6 & 1/6 & 0 & 0 & 0 \\ 1 & 1/3 & 1/3 & 1 & 1/2 & 1/3 & 1/3 & 1/6 & 1/6 & 1/2 & 1/6 & 1/6 \\ \end{bmatrix} \begin{bmatrix} \hat{\mu}\\ \hat{\alpha}_2\\ \hat{\alpha}_3\\ \hat{\beta}_2\\ \hat{\gamma}_2\\ \hat{\theta}_{22}\\ \hat{\theta}_{32}\\ \hat{\tau}_{22}\\ \hat{\tau}_{32}\\ \hat{\psi}_{22}\\ \hat{\lambda}_{222}\\ \hat{\lambda}_{322}\\ \end{bmatrix}. \end{aligned} \]
Esteja ciente de que a matriz \(L_{B}\) que prémultiplica os parâmetros estimados está vínculada ao tipo de restrição paramétrica considerada. Nesta análise foi usado o contraste de tratamento (contr.treatment) que é o padrão do R. Se for usada outra restrição paramétrica, a matriz \(L_{*}\) será diferente mas as médias marginais ainda serão as mesmas porque elas são invariantes à parametrização adotada. A função emmeans() já considera o tipo de contraste na hora de construir a matriz de funções lineares.
# Médias marginais ajustas para o efeito principal de pressão.
emm <- emmeans(m0, specs = ~Pres)## NOTE: Results may be misleading due to involvement in interactionsemm## Pres emmean SE df lower.CL upper.CL
## 25 1.75 0.243 12 1.22 2.28
## 30 4.50 0.243 12 3.97 5.03
##
## Results are averaged over the levels of: Carb, Velo
## Confidence level used: 0.95contrast(emm, method = "pairwise")## contrast estimate SE df t.ratio p.value
## 25 - 30 -2.75 0.344 12 -8.004 <.0001
##
## Results are averaged over the levels of: Carb, VeloAs médias marginais para o efeito de velocidade são obtidas com a seguinte função linear das estimativas dos parâmetros \[ \begin{aligned} \hat{\mu}_\text{C} &= L_{\text{C}} \hat{\beta} \\ \begin{bmatrix} \hat{\mu}_{..1}\\ \hat{\mu}_{..2}\\ \end{bmatrix} &= \begin{bmatrix} 1 & 1/3 & 1/3 & 1/2 & 0 & 1/6 & 1/6 & 0 & 0 & 0 & 0 & 0 \\ 1 & 1/3 & 1/3 & 1/2 & 1 & 1/6 & 1/6 & 1/3 & 1/3 & 1/2 & 1/6 & 1/6 \\ \end{bmatrix} \begin{bmatrix} \hat{\mu}\\ \hat{\alpha}_2\\ \hat{\alpha}_3\\ \hat{\beta}_2\\ \hat{\gamma}_2\\ \hat{\theta}_{22}\\ \hat{\theta}_{32}\\ \hat{\tau}_{22}\\ \hat{\tau}_{32}\\ \hat{\psi}_{22}\\ \hat{\lambda}_{222}\\ \hat{\lambda}_{322}\\ \end{bmatrix}. \end{aligned} \]
# Médias marginais ajustas para o efeito principal de velocidade.
emm <- emmeans(m0, specs = ~Velo)## NOTE: Results may be misleading due to involvement in interactionsemm## Velo emmean SE df lower.CL upper.CL
## 200 2.17 0.243 12 1.64 2.70
## 250 4.08 0.243 12 3.55 4.61
##
## Results are averaged over the levels of: Carb, Pres
## Confidence level used: 0.95contrast(emm, method = "pairwise")## contrast estimate SE df t.ratio p.value
## 200 - 250 -1.92 0.344 12 -5.578 0.0001
##
## Results are averaged over the levels of: Carb, PresComo o objetivo do fabricante é determinar a condição de operação que mais se aproxime do volume de enchimento alvo, no código a seguir são determinadas as médias para cada ponto experimental com o modelo saturado m0.
# Médias de todos os pontos experimentais considerando o modelo maximal.
emm <- emmeans(m0, specs = ~Carb + Pres + Velo) %>%
as.data.frame()
emm %>%
arrange(emmean)## Carb Pres Velo emmean SE df lower.CL upper.CL
## 1 10 25 200 -2.0 0.595119 12 -3.296653 -0.703347
## 2 10 30 200 -0.5 0.595119 12 -1.796653 0.796653
## 3 10 25 250 -0.5 0.595119 12 -1.796653 0.796653
## 4 12 25 200 0.5 0.595119 12 -0.796653 1.796653
## 5 10 30 250 1.0 0.595119 12 -0.296653 2.296653
## 6 12 25 250 1.5 0.595119 12 0.203347 2.796653
## 7 12 30 200 2.5 0.595119 12 1.203347 3.796653
## 8 14 25 200 4.5 0.595119 12 3.203347 5.796653
## 9 12 30 250 5.5 0.595119 12 4.203347 6.796653
## 10 14 25 250 6.5 0.595119 12 5.203347 7.796653
## 11 14 30 200 8.0 0.595119 12 6.703347 9.296653
## 12 14 30 250 10.5 0.595119 12 9.203347 11.796653ps <- position_dodge(0.2)
ggplot(emm, aes(x = Carb, y = emmean, color = Pres, group = Pres)) +
facet_wrap(facets = ~Velo) +
geom_point(position = ps) +
geom_errorbar(aes(ymin = lower.CL, ymax = upper.CL),
position = ps,
width = 0.05) +
labs(x = "Carbonação (%)",
y = "Desvio de volume de enchimento",
color = "Pressão (psi)")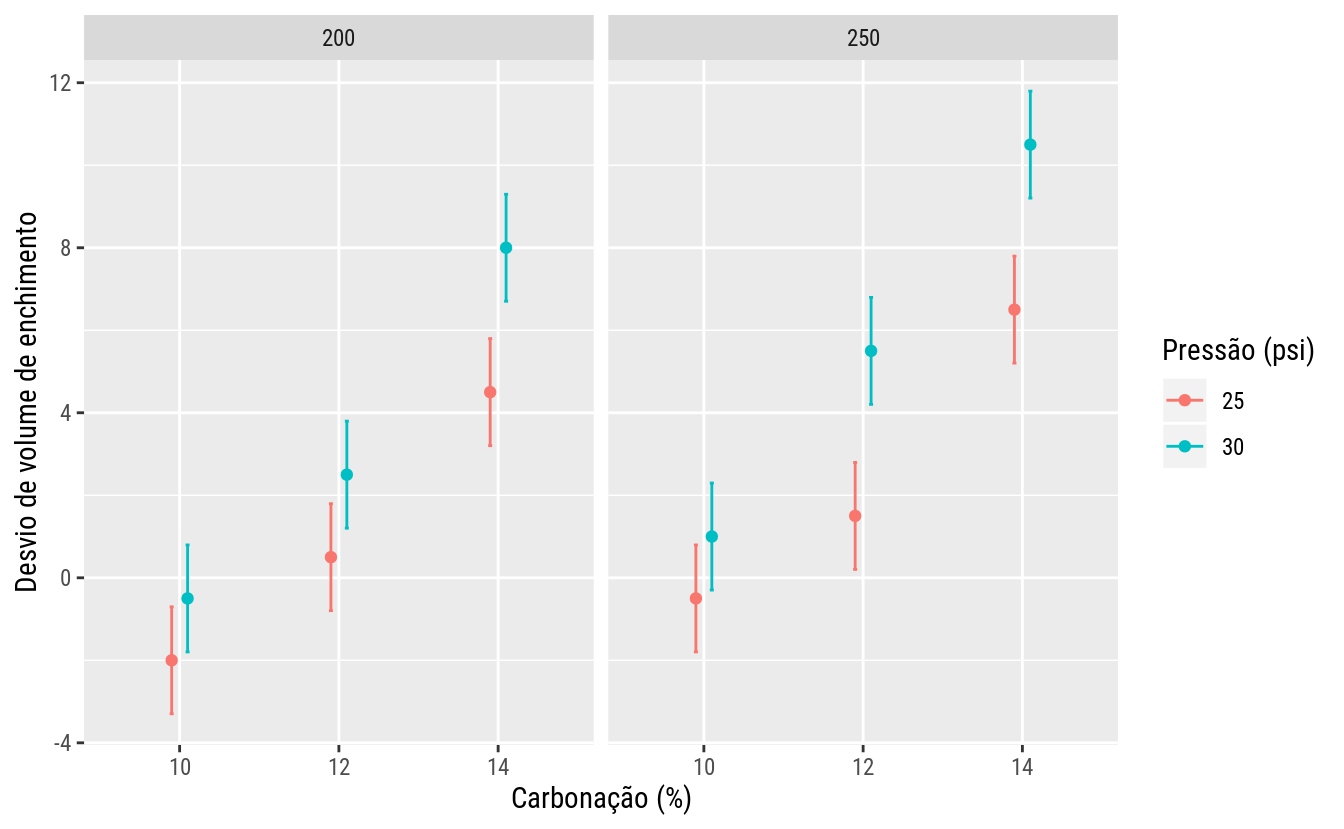
As médias ajustadas com o modelo saturado estão considerando termos do modelo que, pelo quadro de análise de variância, não tem efeito relevante. Dessa forma, um modelo mais simples, obtido pelo abandono dos termos irrelevantes, pode ser ajustado. As médias ajustadas com esse modelo mais simples não deverão distânciar substancialmente do modelo maximal, uma vez que foram abandonados termos irrelevantes para explicar o comportamento médio.
O modelo reduzido é o de efeitos aditivos entre os 3 fatores, ou seja, \[ \begin{aligned} \mu_{ijk} &= \mu + \alpha_i + \beta_j + \gamma_k.\\ \end{aligned} \]
As médias ajustadas, acompanhadas do intervalo de confiança individual de 95% de cobertura, são exibidas no gráfico abaixo. Dos 12 pontos experimentais, 2 apresentam média ajustada com intervalo de confiança que cobre o desvio de enchimento 0. Dessa forma, o pesquisador pode considerar essas condições de operação para o enchimento das garrafas.
# Abandona termos irrelavantes do modelo.
m1 <- update(m0, formula = . ~ Carb + Pres + Velo)
# Médias de todos os pontos experimentais considerando o modelo maximal.
emm <- emmeans(m1, specs = ~Carb + Pres + Velo) %>%
as.data.frame()
emm %>%
arrange(emmean)## Carb Pres Velo emmean SE df lower.CL upper.CL
## 1 10 25 200 -2.83333333 0.4248108 19 -3.7224725 -1.94419420
## 2 10 25 250 -0.91666667 0.4248108 19 -1.8058058 -0.02752753
## 3 10 30 200 -0.08333333 0.4248108 19 -0.9724725 0.80580580
## 4 12 25 200 0.16666667 0.4248108 19 -0.7224725 1.05580580
## 5 10 30 250 1.83333333 0.4248108 19 0.9441942 2.72247247
## 6 12 25 250 2.08333333 0.4248108 19 1.1941942 2.97247247
## 7 12 30 200 2.91666667 0.4248108 19 2.0275275 3.80580580
## 8 12 30 250 4.83333333 0.4248108 19 3.9441942 5.72247247
## 9 14 25 200 5.04166667 0.4248108 19 4.1525275 5.93080580
## 10 14 25 250 6.95833333 0.4248108 19 6.0691942 7.84747247
## 11 14 30 200 7.79166667 0.4248108 19 6.9025275 8.68080580
## 12 14 30 250 9.70833333 0.4248108 19 8.8191942 10.59747247ps <- position_dodge(0.2)
ggplot(emm, aes(x = Carb, y = emmean, color = Pres, group = Pres)) +
facet_wrap(facets = ~Velo) +
geom_point(position = ps) +
geom_errorbar(aes(ymin = lower.CL, ymax = upper.CL),
position = ps,
width = 0.1) +
labs(x = "Carbonação (%)",
y = "Desvio de volume de enchimento",
color = "Pressão (psi)") +
geom_hline(yintercept = 0, lty = 3, col = "black") +
geom_rect(data = filter(emm, abs(emmean) < 0.5),
mapping = aes(xmin = as.integer(Carb) - 0.2,
xmax = as.integer(Carb) + 0.2,
ymin = emmean - 1.25,
ymax = emmean + 1.25),
fill = NA,
lty = 2,
size = 0.3,
position = ps,
show.legend = FALSE)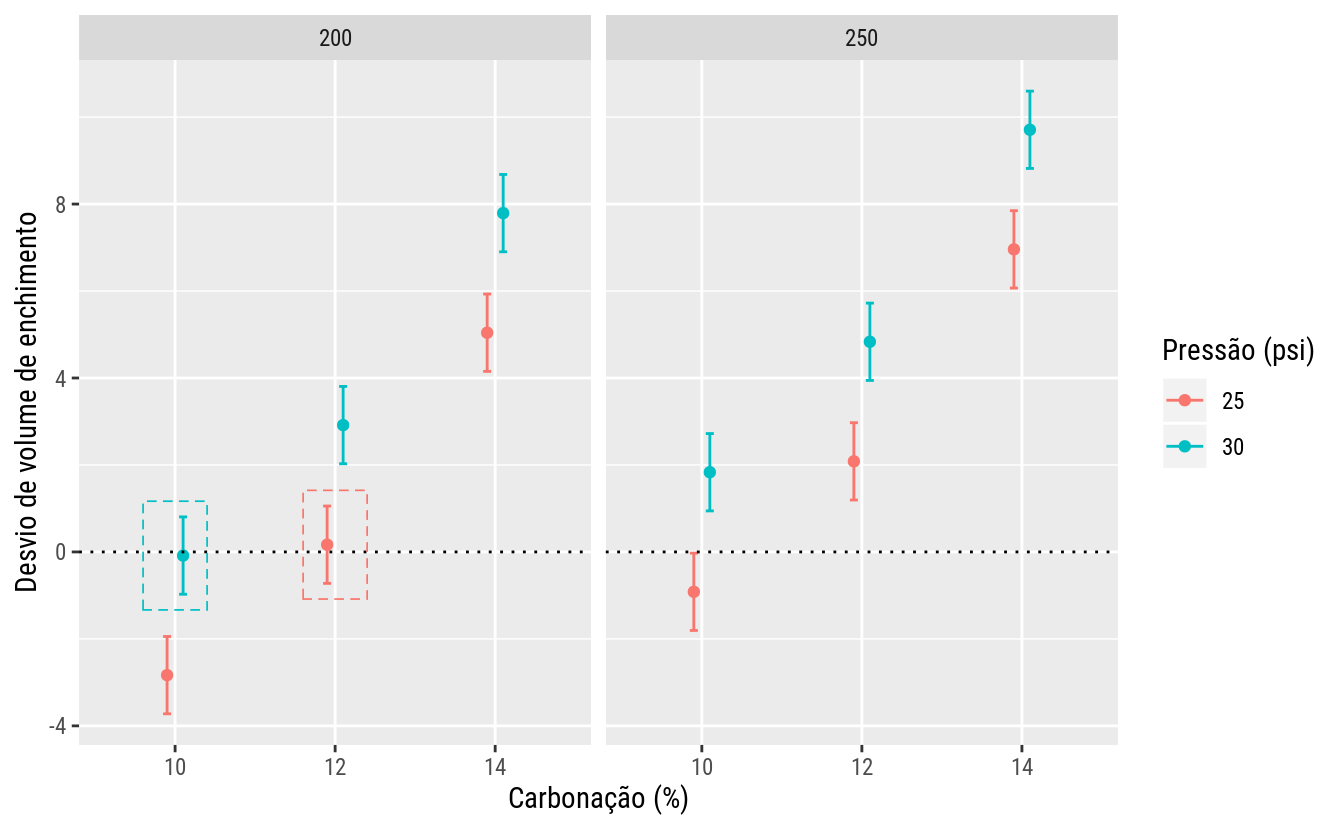
1.4 Considerados finais
Neste capítulo foram introduzidos e analisados experimentos fatoriais gerais com 2 e 3 fatores. Em sala de aula foi discutuda as decisões para realização dos experimentos: casualização, repetição, etc.
Nesse documento foi colocado o modelo estatístico para cada experimento, feitas as contas matriciais para estimação, testes de hipóteses, quadro de análise de variância e médias ajustadas.
Experimentos com 4 fatores também são utilizados em pesquisa científica. No entanto, ocorrem com uma frequência menor. Por essa razão, não serão discutidos nesse capítulo. Nos capítulos seguintes, serão estudados experimentos fatoriais com \(k = 4\) fatores com base 2 e 3.
Referências Bibliográficas
MONTGOMERY, D. Design and analysis of experiments. 7th ed. John Wiley & Sons, 2008.