Capítulo 6 Confundimento para blocagem em fatoriais 2k
6.1 Fundamentação
Existem certas situações em que é praticamente impossível fazer todas as corridas de um experimento em condições uniformes. Por exemplo, pode haver limitações da quantidade de matéria prima, ou matéria prima de diversas origens. As condições de contorno podem mudar ao longo do ensaio (temperatura, ventilação, luz). Pode existir um número elevado de tratamentos difícil de acomodar em um curto espaço de tempo/espaço ou reduzído número de instrumentos/operadores, além de ser desejável variar as condições de contorno para garantir eficiência/robustez aos resultados. A técnica experimental adotada nessas situações é a blocagem.
A blocagem é um recursos para garantir controle local. A idéia central da blocagem é fazer com que as unidades experimentais (UEs) sejam homogêneas dentro dos blocos. Os blocos são completos quando em cada bloco existe pelo menos uma UE de cada ponto experimental, e incompleto caso contrário.
Nos experimentos \(2^k\) existe uma série de opções de blocagem. A primeira é repetir o experimento de forma que cada repetição completa (que inclui todos os pontos experimentais) seja um bloco. É o caso comum quando tem-se poucos tratamentos (geralmente \(2^2\) ou \(2^3\)), e nesses casos específicos temos um fatorial com blocos completos.
Como nos experimentos fatorias \(2^k\) (\(k \geq 3\)) o número de pontos experimentais geralmente é grande, devido ao caráter exploratório do experimento, os blocos dificilmente cumprirão seu papel se forem completos, por isso geralmente adota-se blocos incompletos. Nesse caso os tratamentos devem ser particionados e atribuídos aos blocos. Nada impede que essa partição dos tratamentos seja aleatória, porém quando feita estrategicamente leva-se algumas vantagens.
A estratégia adotada para se atribuir os tratamentos aos blocos é a de confundimento. A idéia central é tomar interações de alta ordem, pois tem menor contribuição pelo princípio da esparsidade, e propositalmente confundir o efeito dessa interação com o efeito dos blocos. Isso porque interações de ordem alta dificilmente são interpretáveis, e o efeito puro dos blocos não é do interesse do pesquisador. O bloco está presente para acomodar alterações das condições de contorno. Dessa forma, não é desconforto ter esses efeitos confundidos/misturados quando o foco do experimento são os efeitos principais e interações de ordem mais baixa.
Vamos considerar a construção e análise de fatoriais \(2^k\) em \(2^p\) blocos incompletos, onde \(p < k\). Consequentemente, estes experimentos podem ser divididos em 2, 4, 8, \(\ldots\) blocos.
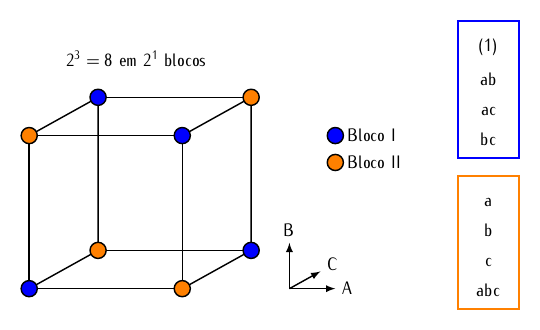
Figura 6.1: Representação geométrica da blocagem feita em um fatorial \(2^3\) para alocação dos pontos experimentais em 2 blocos usando a interação ABC para o confundimento.
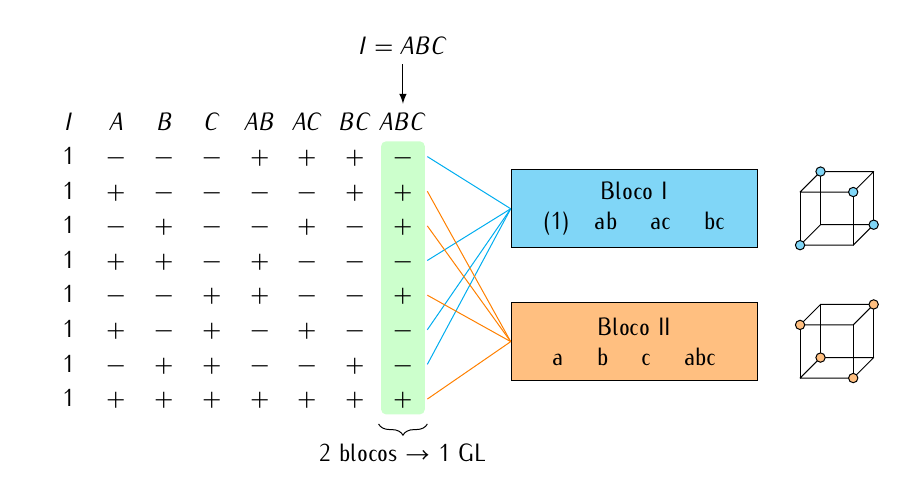
Figura 6.2: Ilustração da alocação dos pontos experimentais de um planejamento fatorial \(2^3\) em 2 blocos usando para o confundimento com os blocos a interação tripla, ou seja, com o contraste de definição \(I = ABC\).

Figura 6.3: Ilustração da alocação dos pontos experimentais de um planejamento fatorial \(2^3\) em 4 blocos usando para o confundimento com os blocos duas interações duplas, no caso, com os contrastes de definição \(I_1 = AB\) e \(I_2 = AC\).
TODO a análise do experimento com blocos completos…
TODO tabela de sinais …
O método mais geral para construir os blocos é através dos contrastes de definição. Esse método é usar para os experimentos fatoriais \(3^k\) também. Este método usa uma combinção linear \[ L = \alpha_1 x_1 + \alpha_2 x_2 + \cdots + \alpha_k x_k, \]
em que \(x_i\) é o nível do \(i\)-ésimo fator aparecendo em um ponto experimental dos \(2^k\) existentes. Nesse contraste, \(x\) está codificado como 0 e 1, para baixo e alto, respectivamente, diferente do tradicional -1 e 1. O coeficiente \(\alpha_i \in \{0, 1\}\) é o expoente aparecendo no \(i\)-ésimo fator no efeito que deve ser confundido.
Por exemplo, se o efeito a ser confundido for ABCD, então os valores de \(\alpha_i\) serão todos iguais a 1, pois \(ABCD = A^1 B^1 C^1 D^1\). Se o efeito a ser confundido for ACD, então os valores serão \(\alpha_1 = \alpha_3 = \alpha_4 = 1\), e \(\alpha_2 = 0\), pois \(ACD = A^1 B^0 C^1 D^1\).
Dessa forma, para o sistema \(2^k\), temos tanto \(\alpha_i = 0\) ou \(1\), e \(x_i = 0\) (nível baixo) ou \(1\) (nível alto). Pontos experimentais que tenham o mesmo valor de \(L \mod 2\) pertencerão ao mesmo bloco. A função \(x \mod 2\) retorna o resto da divisão de \(x\) por 2. Como os únicos valores possíveis de \(L \mod 2\) são 0 e 1, isso atribuirá os \(2^k\) pontos experimentais à exatamente dois blocos.
Como exemplo, considere um planejamento \(2^3\), com a interação ABC (a de ordem mais alta) confundida com bloco. Aqui, \(x_1\) corresponde a A, \(x_2\) a B, e \(x_3\) a C. Portanto, tem-se que \(\alpha_1 = \alpha_2 = \alpha_3 = 1\), pois como o fator a ser confundido é ABC, então o expoente destes três fatores é 1. Portanto, o contraste de definição utilizado para confundir ABC com blocos é \[ L = x_1 + x_2 + x_3. \]
Com a finalidade de atribuir os pontos experimentais aos dois blocos, determina-se o valor de \(L \mod 2\) para cada ponto experimental: \[ \begin{align} (1):& \quad L = 1(0) + 1(0) + 1(0) = 0 \mod 2 = 0 \\ a:& \quad L = 1(1) + 1(0) + 1(0) = 1 \mod 2 = 1 \\ b:& \quad L = 1(0) + 1(1) + 1(0) = 1 \mod 2 = 1 \\ ab:& \quad L = 1(1) + 1(1) + 1(0) = 2 \mod 2 = 0 \\ c:& \quad L = 1(0) + 1(0) + 1(1) = 1 \mod 2 = 1 \\ ac:& \quad L = 1(1) + 1(0) + 1(1) = 2 \mod 2 = 0 \\ bc:& \quad L = 1(0) + 1(1) + 1(1) = 2 \mod 2 = 0 \\ abc:& \quad L = 1(1) + 1(1) + 1(1) = 3 \mod 2 = 1 \end{align} \]
Dessa forma, as combinações (1), ab, ac, e bc são corridas no bloco I, enquanto que a, b, c, e abc são corridas no bloco 2. Veja que esta atribuição é idêntica àquela realizada ao se utilizar a coluna ABC da tabela de sinais. O contraste de definição é apenas uma generalização daquele método.
6.2 Análise do fatorial 24 em 2 blocos
library(tidyverse)Análise dos dados disponíveis no exemplo 7.2, página 310, em MONTGOMERY (2012).
# Criando um experimento 2^4 em dois blocos usando I = ABCD.
k <- 4
da <- do.call(expand.grid,
setNames(replicate(k, c(-1, 1), simplify = FALSE),
LETTERS[1:k]))
# Cria os blocos usando I = ABCD.
da$blc <- with(da,
factor(A * B * C * D,
labels = c("II", "I")))
# Ordena para ficar com a mesma disposição do livro.
da <- da[with(da, order(blc)), ]
da## A B C D blc
## 2 1 -1 -1 -1 II
## 3 -1 1 -1 -1 II
## 5 -1 -1 1 -1 II
## 8 1 1 1 -1 II
## 9 -1 -1 -1 1 II
## 12 1 1 -1 1 II
## 14 1 -1 1 1 II
## 15 -1 1 1 1 II
## 1 -1 -1 -1 -1 I
## 4 1 1 -1 -1 I
## 6 1 -1 1 -1 I
## 7 -1 1 1 -1 I
## 10 1 -1 -1 1 I
## 11 -1 1 -1 1 I
## 13 -1 -1 1 1 I
## 16 1 1 1 1 I# Adiciona o vetor da resposta.
da$y <- c(71, 48, 68, 65, 43, 104, 86, 70,
25, 45, 40, 60, 80, 25, 55, 76)
# Ajuste do modelo saturado.
# m0 <- lm(terms(y ~ A * B * C * D + blc, keep.order = TRUE), data = da)
m0 <- lm(y ~ blc + A * B * C * D,
data = da,
contrasts = list(blc = contr.sum))
# O efeito `A:B:C:D` não foi estimado pois tem um `NA` no lugar.
coef(m0)## (Intercept) blc1 A B C
## 60.0625 9.3125 10.8125 1.5625 4.9375
## D A:B A:C B:C A:D
## 7.3125 0.0625 -9.0625 1.1875 8.3125
## B:D C:D A:B:C A:B:D A:C:D
## -0.1875 -0.5625 0.9375 2.0625 -0.8125
## B:C:D A:B:C:D
## -1.3125 NA# A coluna 2 e a última são linearmente dependentes (= confundimento). E
# o confundimento acontece não importando o tipo de contraste usado.
X <- model.matrix(m0)
prmatrix(model.matrix(m0),
rowlab = rep("", nrow(X)),
collab = rep("", ncol(X)))##
## 1 1 1 -1 -1 -1 -1 -1 1 -1 1 1 1 1 1 -1 -1
## 1 1 -1 1 -1 -1 -1 1 -1 1 -1 1 1 1 -1 1 -1
## 1 1 -1 -1 1 -1 1 -1 -1 1 1 -1 1 -1 1 1 -1
## 1 1 1 1 1 -1 1 1 1 -1 -1 -1 1 -1 -1 -1 -1
## 1 1 -1 -1 -1 1 1 1 1 -1 -1 -1 -1 1 1 1 -1
## 1 1 1 1 -1 1 1 -1 -1 1 1 -1 -1 1 -1 -1 -1
## 1 1 1 -1 1 1 -1 1 -1 1 -1 1 -1 -1 1 -1 -1
## 1 1 -1 1 1 1 -1 -1 1 -1 1 1 -1 -1 -1 1 -1
## 1 -1 -1 -1 -1 -1 1 1 1 1 1 1 -1 -1 -1 -1 1
## 1 -1 1 1 -1 -1 1 -1 -1 -1 -1 1 -1 -1 1 1 1
## 1 -1 1 -1 1 -1 -1 1 -1 -1 1 -1 -1 1 -1 1 1
## 1 -1 -1 1 1 -1 -1 -1 1 1 -1 -1 -1 1 1 -1 1
## 1 -1 1 -1 -1 1 -1 -1 1 1 -1 -1 1 -1 -1 1 1
## 1 -1 -1 1 -1 1 -1 1 -1 -1 1 -1 1 -1 1 -1 1
## 1 -1 -1 -1 1 1 1 -1 -1 -1 -1 1 1 1 -1 -1 1
## 1 -1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1# Cria um tabela com nomes e valores das estimativas.
cfs <- coef(m0)[-(1:2)] %>%
na.omit() %>%
enframe()
# Gráfico quantil-quantil normal das estimativas.
qq <- qqnorm(cfs$value, pch = 19, col = "orange")
text(x = qq$x,
y = qq$y,
labels = cfs$name,
pos = ifelse(qq$x < 0, 4, 2))
# Modelo reduzido.
m1 <- lm(y ~ blc + A * (C + D), data = da)
anova(m1)## Analysis of Variance Table
##
## Response: y
## Df Sum Sq Mean Sq F value Pr(>F)
## blc 1 1387.56 1387.56 66.581 1.889e-05 ***
## A 1 1870.56 1870.56 89.757 5.600e-06 ***
## C 1 390.06 390.06 18.717 0.0019155 **
## D 1 855.56 855.56 41.053 0.0001242 ***
## A:C 1 1314.06 1314.06 63.054 2.349e-05 ***
## A:D 1 1105.56 1105.56 53.049 4.646e-05 ***
## Residuals 9 187.56 20.84
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1# Predição em cada bloco.
predict(m1, newdata = list(blc = "I", A = 1, C = 1, D = 1))## 1
## 73.0625predict(m1, newdata = list(blc = "II", A = 1, C = 1, D = 1))## 1
## 91.6875# Entenda o significado do efeito de bloco na codificação soma 0 com 2
# blocos.
coef(m0)["blc1"] * 2## blc1
## 18.6256.3 Análise do fatorial 25 em 4 blocos
Análise dos dados disponíveis no problema 6-26, página 310, em MONTGOMERY (2012).
An experiment was run in a semiconductor fabrication plant in an effort to increase yield. Five factors, each at two levels, were studied. The factors (and levels) were A aperture setting (small, large), B exposure time (20% below nominal, 20% above nominal), C development time (30 and 45 s), D mask dimension (small, large), and E etch time (14.5 and 15.5 min). The unreplicated 2 raised to 5 design shown below was run.
Um experimento foi realizado em uma planta de fabricação de semicondutores para aumentar o rendimento. Cinco fatores, cada um em dois níveis, foram estudados. Os fatores (e níveis) foram configuração da abertura (A: pequena, grande), tempo de exposição (B: 20% abaixo da nominal, 20% acima da nominal), tempo de desenvolvimento (C: 30 e 45 s), dimensão da máscara (D: pequena, grande), e tempo de gravação (E: 14,5 e 15,5 min). O planejamento fatorial \(2^5\) não replicado foi executado em 4 blocos, usando para o confundimento os efeitos ACDE e BCD.
# Criando um experimento 2^5 não replicado.
k <- 5
da <- do.call(expand.grid,
setNames(replicate(k, c(-1, 1), simplify = FALSE),
LETTERS[1:k]))
attr(da, "out.attrs") <- NULL
# Atribuindo os blocos às corridas.
blc <- factor(with(da, interaction(A * C * D * E, B * C * D)),
labels = as.character(as.roman(1:4)))
# Valores observados.
da$y <- c(7, 9, 34, 55, 16, 20, 40, 60, 8, 10, 32, 50, 18, 21, 44, 61,
8, 12, 35, 52, 15, 22, 45, 65, 6, 10, 30, 53, 15, 20, 41, 63)
m0 <- lm(y ~ blc + A * B * C * D * E, data = da)
# Efeitos não estimados estão com `NA` no lugar.
coef(m0)## (Intercept) blcII blcIII blcIV A
## 30.37500 -0.12500 0.62500 0.12500 5.90625
## B C D E A:B
## 16.96875 4.84375 -0.40625 0.21875 3.96875
## A:C B:C A:D B:D C:D
## 0.21875 0.03125 -0.03125 -0.34375 0.40625
## A:E B:E C:E D:E A:B:C
## 0.46875 0.28125 0.15625 -0.59375 -0.21875
## A:B:D A:C:D B:C:D A:B:E A:C:E
## 0.15625 -0.21875 NA NA 0.15625
## B:C:E A:D:E B:D:E C:D:E A:B:C:D
## 0.46875 0.40625 0.09375 -0.40625 -0.03125
## A:B:C:E A:B:D:E A:C:D:E B:C:D:E A:B:C:D:E
## 0.09375 0.46875 NA -0.46875 -0.09375# A coluna 2 e a última são linearmente dependentes (= confundimento). E
# o confundimento acontece não importando o tipo de contraste usado.
X <- model.matrix(m0)
# Colunas dos efeitos de blocos e interações com os quais foram
# confundidos. São mostradas apenas as linhas distintas.
conf <- c(which(m0$assign == 1),
which(is.na(coef(m0))))
prmatrix(unique(model.matrix(m0)[, conf]),
rowlab = rep("", nrow(X)))## blcII blcIII blcIV B:C:D A:B:E A:C:D:E
## 1 0 0 -1 -1 1
## 0 0 0 -1 1 -1
## 0 0 1 1 1 1
## 0 1 0 1 -1 -1# NOTE: Não é mais uma relação um para um. Ou seja, 3 efeitos se
# confundem com os outros 3 efeitos, mas não em uma relação em que
# existam pares correspondentes.
# Cria um tabela com nomes e valores das estimativas.
cfs <- coef(m0)[m0$assign > 1] %>%
na.omit() %>%
enframe()
# Gráfico quantil-quantil normal das estimativas.
qq <- qqnorm(cfs$value, pch = 19, col = "orange")
text(x = qq$x,
y = qq$y,
labels = cfs$name,
pos = ifelse(qq$x < 0, 4, 2))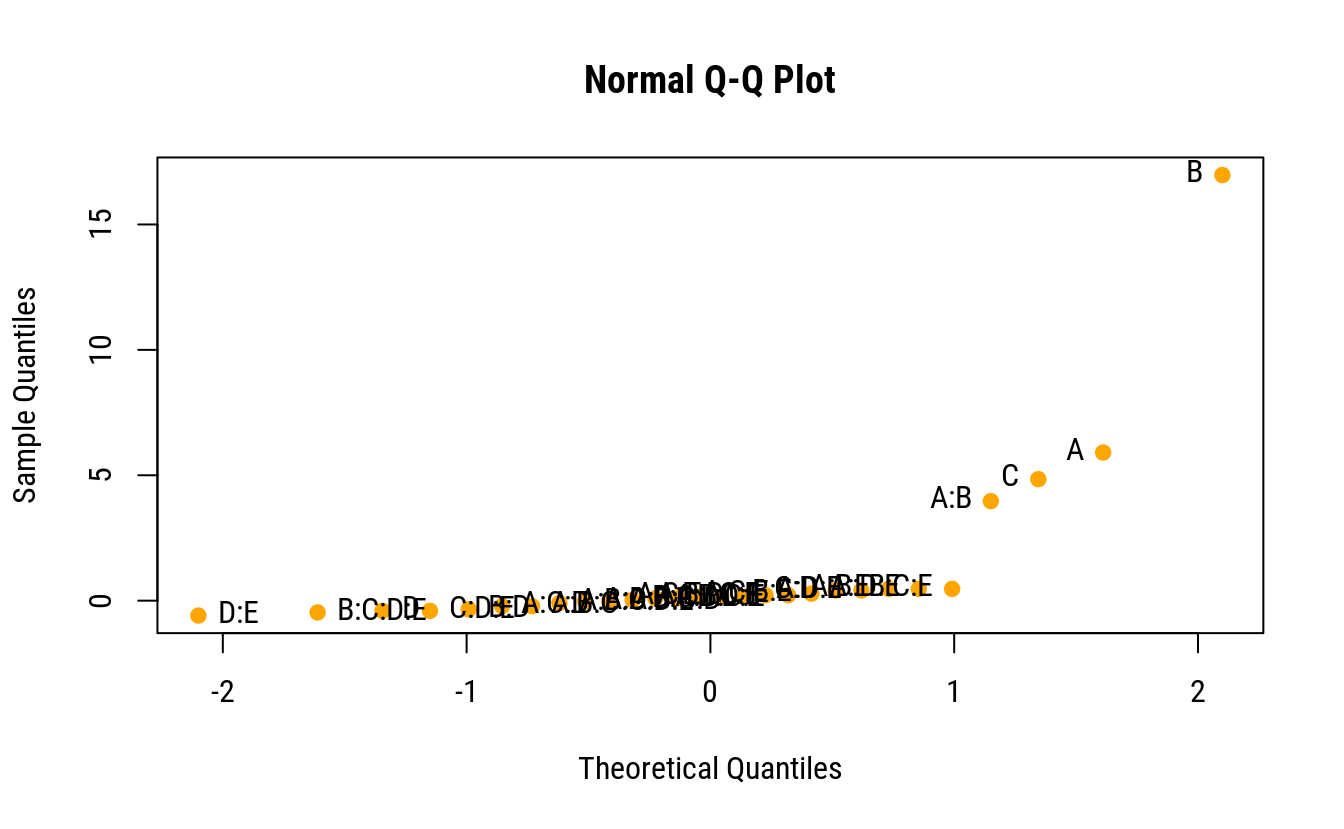
m1 <- lm(y ~ blc + A + B + C + D + A:B + D:E + B:C, data = da)
anova(m1)## Analysis of Variance Table
##
## Response: y
## Df Sum Sq Mean Sq F value Pr(>F)
## blc 3 2.6 0.9 0.3043 0.82192
## A 1 1116.3 1116.3 392.9497 4.480e-15 ***
## B 1 9214.0 9214.0 3243.4935 < 2.2e-16 ***
## C 1 750.8 750.8 264.2876 2.257e-13 ***
## D 1 5.3 5.3 1.8591 0.18717
## A:B 1 504.0 504.0 177.4274 1.038e-11 ***
## D:E 1 11.3 11.3 3.9712 0.05944 .
## B:C 1 0.0 0.0 0.0110 0.91746
## Residuals 21 59.7 2.8
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 16.4 Confundimento parcial
Análise dos dados disponíveis no exemplo 7.3, página 318, em MONTGOMERY (2012).
# Valores digitados conforme disposição na ilustração do livro.
dat <- c(0, 0, 0, 0, 0, 550,
1, 1, 0, 0, 0, 642,
1, 0, 1, 0, 0, 749,
0, 1, 1, 0, 0, 1075,
1, 0, 0, 1, 0, 669,
0, 1, 0, 1, 0, 633,
0, 0, 1, 1, 0, 1037,
1, 1, 1, 1, 0, 729,
0, 0, 0, 0, 1, 604,
0, 0, 1, 0, 1, 1052,
1, 1, 0, 0, 1, 635,
1, 1, 1, 0, 1, 860,
1, 0, 0, 1, 1, 650,
0, 1, 0, 1, 1, 601,
1, 0, 1, 1, 1, 868,
0, 1, 1, 1, 1, 1063)
da <- matrix(dat, ncol = 6, byrow = TRUE)
da <- as.data.frame(da)
names(da) <- c("A", "B", "C", "blc", "rpt", "y")
da <- transform(da,
A = 2 * (A - 0.5),
B = 2 * (B - 0.5),
C = 2 * (C - 0.5),
blc = factor(blc),
rpt = factor(rpt))
str(da)## 'data.frame': 16 obs. of 6 variables:
## $ A : num -1 1 1 -1 1 -1 -1 1 -1 -1 ...
## $ B : num -1 1 -1 1 -1 1 -1 1 -1 -1 ...
## $ C : num -1 -1 1 1 -1 -1 1 1 -1 1 ...
## $ blc: Factor w/ 2 levels "0","1": 1 1 1 1 2 2 2 2 1 1 ...
## $ rpt: Factor w/ 2 levels "0","1": 1 1 1 1 1 1 1 1 2 2 ...
## $ y : num 550 642 749 1075 669 ...# Modelo com efeito de blocos dentro de repetições para um planejamento
# fatorial 2^3 usando em cada repetição I = ABC e I = AB,
# respectivamente.
# m0 <- lm(y ~ rpt/blc + A * B * C, data = da)
m0 <- lm(terms(y ~ rpt/blc+ A + B + C + A:B + A:C + B:C + A:B:C,
keep.order = TRUE),
data = da)
# Todos os efeitos foram estimados.
summary(m0)##
## Call:
## lm(formula = terms(y ~ rpt/blc + A + B + C + A:B + A:C + B:C +
## A:B:C, keep.order = TRUE), data = da)
##
## Residuals:
## 1 2 3 4 5 6 7
## 0.8125 31.3125 -48.8125 16.6875 12.8125 19.3125 12.9375
## 8 9 10 11 12 13 14
## -45.0625 -0.8125 -12.9375 -31.3125 45.0625 -12.8125 -19.3125
## 15 16
## 48.8125 -16.6875
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 753.125 30.929 24.350 2.18e-06 ***
## rpt1 55.625 43.740 1.272 0.25942
## rpt0:blc1 14.750 50.507 0.292 0.78199
## rpt1:blc1 -34.250 50.507 -0.678 0.52780
## A -50.812 12.627 -4.024 0.01008 *
## B 3.688 12.627 0.292 0.78199
## C 153.062 12.627 12.122 6.75e-05 ***
## A:B -21.000 17.857 -1.176 0.29253
## A:C -76.812 12.627 -6.083 0.00174 **
## B:C -1.062 12.627 -0.084 0.93621
## A:B:C -0.875 17.857 -0.049 0.96282
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 50.51 on 5 degrees of freedom
## Multiple R-squared: 0.976, Adjusted R-squared: 0.928
## F-statistic: 20.33 on 10 and 5 DF, p-value: 0.001954# NOTE: todos os efeitos foram estimados, porém, e existe diferença no
# erro padrão. Como essa informação poder ser aproveitada para o
# planejamento de experimentos?
# Quando de anova completo.
anova(m0)## Analysis of Variance Table
##
## Response: y
## Df Sum Sq Mean Sq F value Pr(>F)
## rpt 1 3875 3875 1.5191 0.272551
## rpt:blc 2 458 229 0.0898 0.915560
## A 1 41311 41311 16.1941 0.010079 *
## B 1 218 218 0.0853 0.781987
## C 1 374850 374850 146.9446 6.749e-05 ***
## A:B 1 3528 3528 1.3830 0.292529
## A:C 1 94403 94403 37.0066 0.001736 **
## B:C 1 18 18 0.0071 0.936205
## A:B:C 1 6 6 0.0024 0.962816
## Residuals 5 12755 2551
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1# Determine os efeitos confundidos com bloco em cada repetição
# inspecionando a matriz do modelo.
X <- model.matrix(m0)
prmatrix(model.matrix(m0)[with(da, rpt == "0"), ],
rowlab = rep("", nrow(X)))## (Intercept) rpt1 rpt0:blc1 rpt1:blc1 A B C A:B A:C B:C A:B:C
## 1 0 0 0 -1 -1 -1 1 1 1 -1
## 1 0 0 0 1 1 -1 1 -1 -1 -1
## 1 0 0 0 1 -1 1 -1 1 -1 -1
## 1 0 0 0 -1 1 1 -1 -1 1 -1
## 1 0 1 0 1 -1 -1 -1 -1 1 1
## 1 0 1 0 -1 1 -1 -1 1 -1 1
## 1 0 1 0 -1 -1 1 1 -1 -1 1
## 1 0 1 0 1 1 1 1 1 1 1prmatrix(model.matrix(m0)[with(da, rpt == "1"), ],
rowlab = rep("", nrow(X)))## (Intercept) rpt1 rpt0:blc1 rpt1:blc1 A B C A:B A:C B:C A:B:C
## 1 1 0 0 -1 -1 -1 1 1 1 -1
## 1 1 0 0 -1 -1 1 1 -1 -1 1
## 1 1 0 0 1 1 -1 1 -1 -1 -1
## 1 1 0 0 1 1 1 1 1 1 1
## 1 1 0 1 1 -1 -1 -1 -1 1 1
## 1 1 0 1 -1 1 -1 -1 1 -1 1
## 1 1 0 1 1 -1 1 -1 1 -1 -1
## 1 1 0 1 -1 1 1 -1 -1 1 -1# Modelo final.
m1 <- lm(terms(y ~ rpt/blc + A * C, keep.order = TRUE), data = da)
anova(m1, m0)## Analysis of Variance Table
##
## Model 1: y ~ rpt/blc + A * C
## Model 2: y ~ rpt/blc + A + B + C + A:B + A:C + B:C + A:B:C
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 9 16525
## 2 5 12755 4 3769.8 0.3694 0.822anova(m1)## Analysis of Variance Table
##
## Response: y
## Df Sum Sq Mean Sq F value Pr(>F)
## rpt 1 3875 3875 2.1105 0.180246
## rpt:blc 2 458 229 0.1248 0.884211
## A 1 41311 41311 22.4995 0.001054 **
## C 1 374850 374850 204.1598 1.719e-07 ***
## A:C 1 94403 94403 51.4158 5.248e-05 ***
## Residuals 9 16525 1836
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 16.5 Material complementar
Referências Bibliográficas
MONTGOMERY, D. C. Design and analysis of experiments. 8th ed. New York: John Wiley & Sons, 2012.