Capítulo 2 Experimentos fatoriais 2k
2.1 Visão geral
Os experimentos fatoriais \(2^k\) são uma categoria especial dos experimentos fatoriais gerais. Usa-se essa nomenclatura para indicar que são estudados \(k\) fatores, cada um deles com 2 níveis, de forma completamente cruzada, perfazendo \(p\) pontos experimentais.
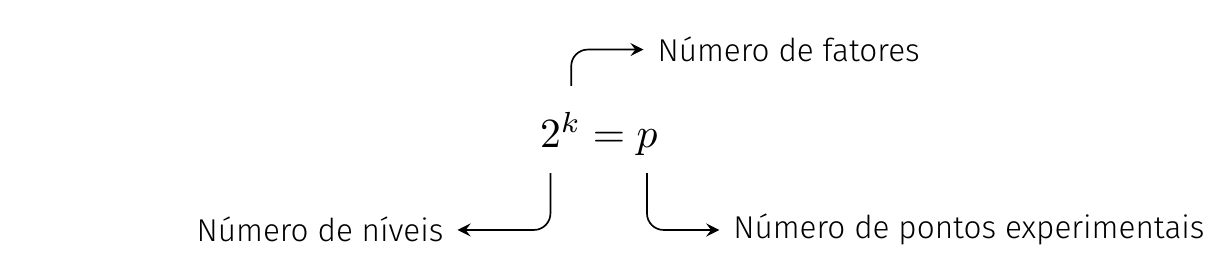
Para estudar o efeito de um fator é preciso que se tenha no mínimos dois níveis. Dessa forma, o fatorial \(2^k\) é o mais econômico tipo de experimento fatorial. O número de pontos experimentais cresce numa progressão geométrica de razão 2. O \(2^k\) é útil para investigar simultaneamente vários fatores para posteriormente afunilar a investigação naqueles que se mostragem mais relevantes. O nome dado para esse experimento é screening designs ou screening experiments.
Os experimentos de triagem (screening) são feitos nas etapas iniciais de uma nova investigação quando não se sabe exatamente quais dos \(k\) fatores previamente listados influenciam a resposta de um fenômeno. Para que se possa, portanto, considerar os vários fatores simultaneamente sem elevar o custo experimental com muitos pontos experimentais, usa-se 2 níveis para cada um dos \(k\) fatores.
O fatorial \(2^k\) é interessante para
- (\(2^k\) completo com \(r > 1\) repetições) Estudar poucos fatores (\(k = 2, \ldots, 4\)) fazendo \(r\) repetições de cada ponto experimental. Isso dá um experimento com \(r2^k\) corridas ou unidades experimentais que, em situações com uniformidade de unidades/condições experimentais pode-se fazer em delineamento inteiramente casualizado.
- (\(2^k\) completo com \(r = 1\) repetição) Estudar vários fatores (\(k \geq 4\)) com uma única réplica para cada ponto experimental (\(r = 1\)) e, ao considerar o efeito interações de alta como nulos, a partir delas estimar a variância do erro para testar os efeitos.
- (\(2^k\) completo em \(b = 2^{k - u}\) blocos, \(u < k\)) Estudar \(k\) fatores com \(r \geq 1\) repetições dos pontos experimentais fazendo-se a blocagem para acomodar variações das unidades/condições experimentais. Se o tamanho do bloco for múltiplo de 2 mas menor que \(2^k\), ou seja \(2^u\) com \(u < k\), pode-se usar a técnica de confundimento para escolher as corridas experimentais que devem ser atribuídas às \(u\) unidades experimentais de cada bloco. Dessa forma, o experimento terá \(r2^k\) unidades experimentais alocadas em \(b = \frac{r2^k}{2^u} = r2^{k - u}\) blocos.
- (fração de \(2^k\) com \(2^u\) unidades experimentais, \(u < k\)) Estudar \(k\) fatores com apenas \(2^u (u < k)\) corridas/unidades experimentais. Como não há disponibilidade de recursos para ou interesse em estudar todos os \(2^k\) pontos experimentais, estuda-se uma fração \(2^{k - u}\) deles. Todavia, os pontos experimentais presentes nessa fração não são uma coleção aleatória qualquer, mas sim pontos experimentais devidamente escolhidos para que o delineamento apresente boas propriedades.
- (\(2^k\) com \(a > 1\) pontos adicionais) Estudar \(k\) fatores quantitativos em um esquema de planejamento evolucionário de experimento. É a situação que visa determinar a condição de operação ótima, ou seja, o conjunto de valores \(x_i (i = 1, \ldots, k\)) no domínio de cada um dos \(k\) fatores em que a resposta é ótima. Para isso usa delineamentos com pontos experimentais adicionais. O mais simples é o que adiciona apenas \(a\) corridas/unidades experimentais no ponto central (centro da região experimental).
As 5 situações acima descritas serão estudadas nesse curso.
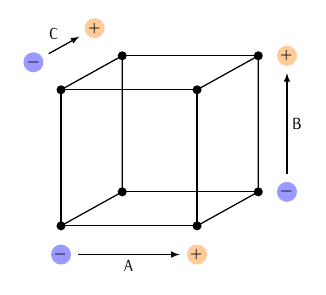
Figura 2.1: Experimento em planejamento fatorial \(2^3\).
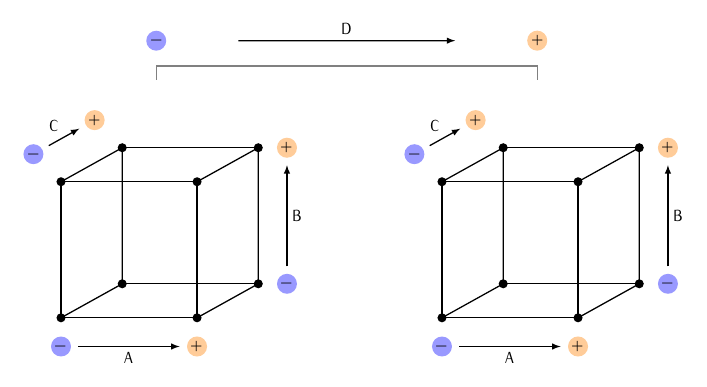
Figura 2.2: Experimento em planejamento fatorial \(2^4\).

Figura 2.3: Experimento em planejamento fatorial \(2^5\).
2.2 Modelo estatístico
Considerando o experimento fatorial \(2^k\) completo, o modelo estatístico que considera todas os termos de interação até a ordem \(k\) terá

Por simplicidade de exposição, considere \(k = 3\). O modelo estatístico é \[ \begin{align*} y_{ijkr}|ijk &\sim \text{Normal}(\mu_{ijk}, \sigma^2)\\ \mu_{ijk} &= \mu + A_i + B_j + C_k + (AB)_{ik} + (AC)_{ik} + (BC)_{jk} + (ABC)_{ijk}\\ \sigma^2 &\propto 1. \end{align*} \]
Preferiu-se usar letras romanas no lugar de gregas para indicar o conjunto de parâmetros de cada termo. Dentro da expressão do modelo \(k\) é o subíndice do fator C e não o número de fatores. Para não haver confusão, entenda que \((AB)\) é a indicação de esse termo acomoda o efeito do produto cruzado dos fatores A e B e não que seja o produto de dois números \(A\) e \(B\).
Se cada ponto experimental tiver \(r > 1\) repetições, então tem-se um estimador puro do erro experimental \(\sigma^2\) baseado em \(2^k(r - 1)\) graus de liberdade. É muito importante destacar esse aspector. Estimador puro do erro experimental é aquele proveniente apenas dos desvios das repetições dentro de cada ponto experimental. Ele não tem “impurezas”, ou melhor, contribuições de termos omitidos do modelo da média \(\mu_{ijk}\). Para experimentos \(2^k\) completos com \(r = 1\) repetição, o estimador do erro experimental não será puro mas sim composto por termos omitidos do modelo da média, no caso, interações de ordem alta.

Figura 2.4: Esquema do quadro de análise de variância para um experimento fatorial \(2^k\) completo com \(r\) repetições.
2.3 Nomenclatura alfabética para os pontos experimentais
Para se referir aos pontos experimentais de um experimento \(2^k\) usa-se a nomenclatura alfabética indicada no quadro a seguir. A nomenclatura posicional incremental também é empregada, porém, mais frequente em experimentos \(3^k\).

Figura 2.5: Nomenclatura alfabética e posicional incremental em um experimento fatorial \(2^3\).
A nomenclatura indica que o fator aparece no ponto experimental com nível alto quando a letra do alfabeto minúsculo que o representa estiver aparecendo. Caso contrário, o fator aparece no nível baixo. Nível alto é o segundo nível, e.g. \(a_2\), nível baixo é o primeiro, e.g. \(a_1\). Quando todos os fatores então no nível baixo, usa-se \((1)\).
A notação posicional incremental é muito simples. Os níveis de um fator são codificados em \(0, \ldots, k - 1\). Para \(2^k\), o número 0 indica que o fator está no nível baixo e o 1 indica que está no nível alto. Essa notação é útil para construção de delineamentos com confundimento e fracionamento dos pontos experimentais.
2.4 Codificação para a matriz do modelo
Uma vez espeficado o modelo, existem diferentes opções de codificação que podem ser usadas conforme o tipo dos fatores: qualitativo ou quantitativo. No entanto, como o número de níveis de cada fator é 1, o máximo número de parâmetros necessários para acomodar o efeito de um fator é 1, seja ele qualitativo ou quantitativo. O que muda é apenas a interpretação e a possibilidade de fazer predições além dos níveis estudados dos fatores.
Quando um fator é qualitativo pode-se usar a codificação de tratamento. Nela, o parâmetro associado ao primeiro nível de cada fator considerado 0. Os parâmetros tem interpretação de diferença em relação ao ponto experimental de referência. Essa codificação, embora muito muito utilizada é subótima no sentido de não gerar uma base ortogonal de vetores coluna na matriz do modelo. Veja o topo da Figura 2.6.
Quando o fator é quantitativo, pode-se definir a matriz do modelo usando os próprios níveis numéricos, com cada fator sendo representado na sua própria escala e unidade de medida. Essa representação, embora usada sem preocupação em problemas de regressão, é subótima porque a matriz \(X^\top X\) é densa. Além disso, a interpretação dos parâmetros e o erro-padrão associado às estimativas será dependente da escala dos fatores. Pode-se facilitar a análise do experimento usando um esquema de codificação apropriado. Veja o meio da Figura 2.6.
Para tirar vantagem de benefícios computacionais e de interpretação, usa-se codificar os níveis dos fatores com \(-1\) para o primeiro nível e \(+1\) para o segundo. Essa codificação corresponde ao contraste soma zero se o fator for qualitativo. Se o fator for quantitativo corresponde à uma padronização de escala para ter ponto central em 0 e amplitude 1. A operação de transformação é bem simples \[ z = 2 \cdot \frac{x - (x_1 + x_2)/2}{x_2 - x_1}, \quad z \in \{0, 1\}, \] em que \(x\) é o fator na escala original sendo \(x_1\) e \(x_2\) seus níveis baixo e alto, respectivamente, e \(z\) o fator na escala codificada, com nível baixo representado por \(-1\) e alto por \(+1\).
Com a parametrização centrada, tem-se então, i) mais comodidade computacional pois o produto interno entre colunas da matriz do modelo é 0, gerando uma matriz diagonal fácil de obter a inversa e ii) interpretação comparativa dos efeitos, ou seja, uma vez que os fatores estão sob a mesma escala, as estimativas de maior tamanho absoluto correspondem aos termos de maior efeito e iii) os erros-padrões das estimativas serão todos de mesmo tamanho, o que decorre da diagonal homogênea de \(X^\top X\).

Figura 2.6: Tipos de codificação usadas para representar o efeito de fatores em experimentos fatoriais \(2^k\).
A codificação soma zero gera uma base ortogonal, com isso as colunas são ortogonais entre si.
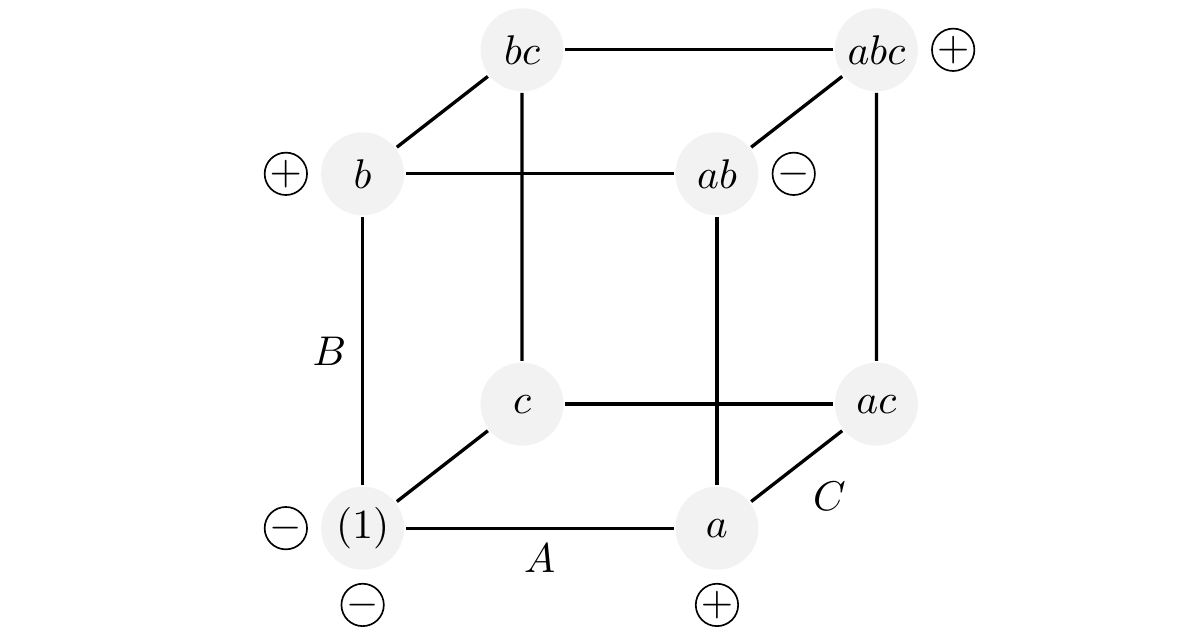
2.5 Representação geométrica
Considerando o fatorial \(2^3\), a representação geométrica indica os pontos experimentais no espaço \(k\)-dimensional. Os vértices estão sob as coordenadas \(-1\) e \(+1\) em cada um dos eixos.
2.6 Estimação dos efeitos
O modelo estatístico corresponde ao experimento fatorial declarado acima é linear nos parâmetros. Dessa forma, a estimação dos parâmetros pelo método de mínimos quadrados ordinários é feita por \[ \hat{\beta} = (X^\top X)^{-1} (X^\top y). \]
A variância das estimativas é obtida por \[ \text{Var}(\hat{\beta}) = \sigma^2 \text{diag}((X^\top X)^{-1}). \]
Quando a matriz \(X\) é a matriz de sinais decorrente da codificação com pontos de suporte em \(-1\) e \(+1\), pode-se facilmente estimar os parâmetros por meio de contrastes entre grupos de médias (Figura 2.7).

Figura 2.7: Estimação dos parâmetros do modelo para o experimento fatorial \(2^3\) com \(r = 1\) repetições.
Pode-se facilmente compreender que os efeitos estimados são funções lineares dos valores observados nos pontos experimentais. Para ser mais específico, são contrastes entre dois grupos de médias amostrais. A figura 2.8 exibe geometricamente o conjunto de pontos experimentais considerado em cada um dos termos do contraste.
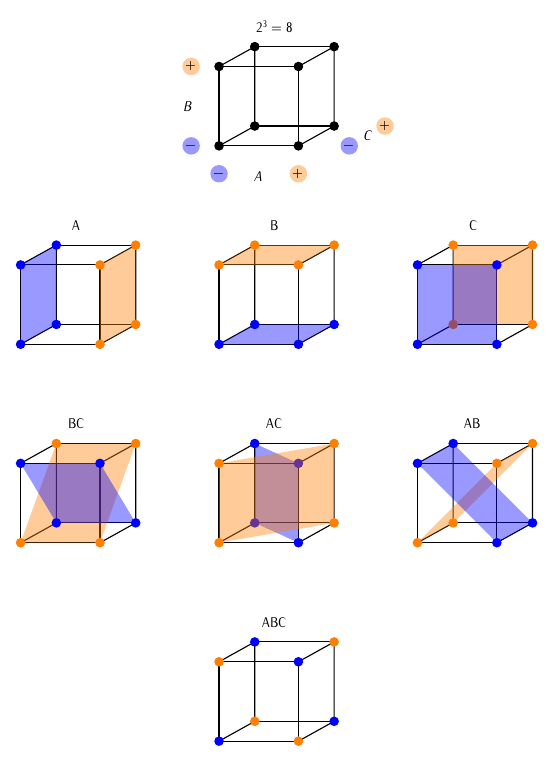
Figura 2.8: Ilustração geométrica de como os efeitos são determinados a partir dos pontos experimentais do delineamento.
2.7 Testes de hipótese
Recordando que a expressão do modelo é \[ \begin{align*} \mu_{ijk} &= \mu + A_i + B_j + C_k + (AB)_{ik} + (AC)_{ik} + (BC)_{jk} + (ABC)_{ijk},\\ \end{align*} \] as hipóteses sobre o efeito dos termos experimentais são \[ \begin{align*} H_0^A&: A_i = 0 \,\,\forall i \quad \Rightarrow \quad H_0^A: \mu_{A+} - \mu_{A-} = 0\\ H_0^B&: B_j = 0 \,\,\forall j \quad \Rightarrow \quad H_0^B: \mu_{B+} - \mu_{B-} = 0\\ H_0^C&: C_k = 0 \,\,\forall k \quad \Rightarrow \quad H_0^C: \mu_{C+} - \mu_{C-} = 0\\ H_0^{AB}&: (AB)_{ij} = 0 \,\,\forall ij\\ & \vdots \\ H_0^{ABC}&: (ABC)_{ijk} = 0 \,\,\forall ijk\\ \end{align*} \]
Tais hipóteses tem um grau de liberdade cada. Elas podem ser igualmente testadas pela estatística \(F\) do quadro de análise de variância quando pela estatística \(t\) do quadro de resumo de parâmetros estimados. Lembre-se que para estatísticas de teste com 1 grau de liberdade, uma estatística \(t\) ao quadrado, \(t^2\), tem distribuição \(F\).
2.8 Somas de quadrados
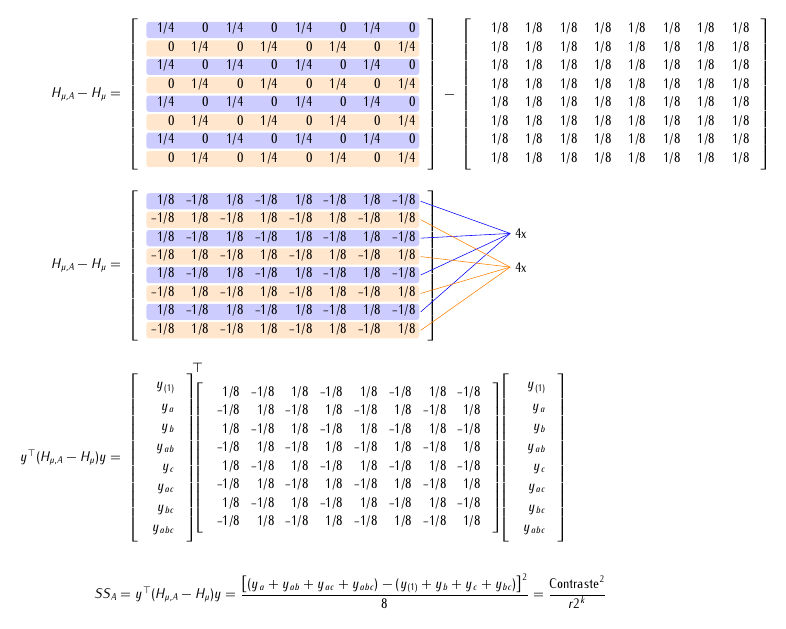
Figura 2.9: Ilustração da obtenção da soma de quadrados de um efeito pelas expressões matriciais e sua redução em expressão baseada no quadrado do contraste entre médias.